Up: AC RC Circuits
Previous: The Differential Equation
From the point of view of the power supply,21.5the circuit is a "black box" that "resists" the applied voltage
with a rather weird "back 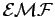 "
"
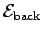 given by
given by 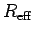 times the current
times the current 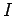 ;
;
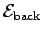 is given by the sum of both terms in Eq. (11)
or the sum of the two vectors in Fig. 21.2.
The power dissipated in the circuit is
the product of the real part of the applied voltage21.6
and the real part of the resultant current21.7
is given by the sum of both terms in Eq. (11)
or the sum of the two vectors in Fig. 21.2.
The power dissipated in the circuit is
the product of the real part of the applied voltage21.6
and the real part of the resultant current21.7
which oscillates at a frequency 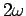 between zero and its maximum value
between zero and its maximum value
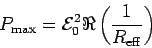 |
(21.13) |
so that the average power drain is21.8
![\begin{displaymath}
\langle P \rangle = {1\over2} {\cal E}_0^2
\left[ R \over R^2 + X_C^2 \right] \; .
\end{displaymath}](img45.gif) |
(21.14) |
A little more algebra will yield the practical formula
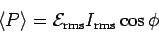 |
(21.15) |
where
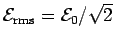 ,
,
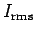 is the root-mean-square current in the circuit,
is the root-mean-square current in the circuit,
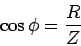 |
(21.16) |
is the "power factor" of the 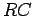 circuit and
circuit and
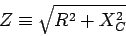 |
(21.17) |
is the impedance of the circuit.21.9
This gets a lot more interesting when we add
the "inertial" effects of inductance
to our circuit. Stay tuned.
Footnotes
- . . . supply,21.5
- Please
forgive my anthropomorphization of circuit elements;
these metaphors help me remember their "behaviour".
- . . . voltage21.6
- The
imaginary voltage component doesn't generate any power.
- . . . current21.7
- Neither
does the imaginary part of the current.
- . . . is21.8
- I have used
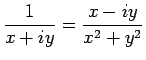 to obtain the real part of
to obtain the real part of 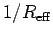 .
.
- . . . circuit.21.9
- Expressing
the average power dissipation in this form
allows one to think of an AC
 circuit
the same way as a DC
circuit
the same way as a DC 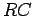 circuit
with the power factor as a sort of
"fudge factor".
circuit
with the power factor as a sort of
"fudge factor".


Up: AC RC Circuits
Previous: The Differential Equation
Jess H. Brewer -
Last modified: Mon Nov 16 18:13:36 PST 2015
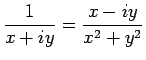 to obtain the real part of
to obtain the real part of