- . . . )?"11.1
- This
is a lot like knowing that 6 is some number n multiplied by 2
and asking what n is. We figure this out by asking ourselves
the question, "What do I have to multiply by 2 to get 6?"
Later on we learn to call this "division" and express the question
in the form, "What is n = 6/2?" but we might just as well call it
"anti-multiplication" because that is how we solve it (unless it is
too hard to do in our heads and we have to resort to some complicated
technology like long division).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
one.11.2
- Any introductory Calculus text
will explain what an integral "means" in terms of visual pictures
that the right hemisphere can handle easily:
whereas the derivative of f(x) is the slope
of the curve, the integral of g(x) is
the area under the curve.
This helps to visualize the integral as the limiting case of
a summation: imagine the area under the curve of g(x)
from x0 to x being divided up into N rectangular columns
of equal width
 and height g(xn),
where
and height g(xn),
where
 is the position of the
is the position of the
 column.
If N is a small number, then
column.
If N is a small number, then
 is a crude approximation to the area under the smooth curve;
but as N gets bigger, the columns get skinnier
and the approximation becomes more and more accurate
and is eventually (as
is a crude approximation to the area under the smooth curve;
but as N gets bigger, the columns get skinnier
and the approximation becomes more and more accurate
and is eventually (as
 )
exact!
This is the meaning of the integral sign:
)
exact!
This is the meaning of the integral sign:
Why do I put this nice graphical description in a footnote?
Because we can understand most of the Physics applications of integrals
by thinking of them as "antiderivatives"
and because when we go to solve an integral we almost always
do it by asking the question, "What function is this the derivative of?"
which means thinking of integrals as antiderivatives.
This is not a complete description of the mathematics,
but it is sufficient for the purposes of this course.
[See? We really do "deemphasize mathematics!"]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . itself,11.3
- This
also holds for the integrals of differentials of vectors.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . Newton.11.4
- It should be remembered
that René Descartes and Christian Huygens formulated
the LAW OF CONSERVATION OF MOMENTUM before
Newton's work on Mechanics. They probably deserve to be
remembered as the First Modern Conservationists!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . position11.5
- In
the section on CIRCULAR MOTION
we chose
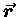 to denote the vector position of a particle
in a circular orbit, using the centre of the circle as the origin
for the
to denote the vector position of a particle
in a circular orbit, using the centre of the circle as the origin
for the
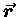 vector.
Here we are switching to
vector.
Here we are switching to
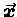 to emphasize that the current description works equally well
for any type of motion, circular or otherwise.
The two notations are interchangeable, but we tend to prefer
to emphasize that the current description works equally well
for any type of motion, circular or otherwise.
The two notations are interchangeable, but we tend to prefer
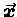 when we are talking mainly about rectilinear
(straight-line) motion and
when we are talking mainly about rectilinear
(straight-line) motion and
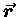 when we are referring our coordinates to
some centre or axis.
when we are referring our coordinates to
some centre or axis.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . ball.11.6
- It is unfortunate that
the conventional symbol for the weight,
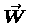 ,
uses the same letter as the conventional symbol for the
work, W. I will try to keep this straight by
referring to the weight always and only in its vector
form and reserving the scalar W for the work.
But this sort of difficulty is eventually inevitable.
,
uses the same letter as the conventional symbol for the
work, W. I will try to keep this straight by
referring to the weight always and only in its vector
form and reserving the scalar W for the work.
But this sort of difficulty is eventually inevitable.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . point.11.7
- For now, I specifically exclude
cases where the ball gets going so fast that it does
get airborne at some places.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . upward.11.8
- Alas,
another unfortunate juxtaposition of symbols!
We are using
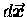 to describe the differential vector
position change and dy to describe the vertical component
of
to describe the differential vector
position change and dy to describe the vertical component
of
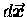 .
Fortunately we have no cause to talk about the
horizontal component in this context, or we might wish we had
used
.
Fortunately we have no cause to talk about the
horizontal component in this context, or we might wish we had
used
 after all!
after all!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . spring11.9
- It is important
to keep careful track of who is doing work on whom,
especially in this case, because if you are careless the minus signs
start jumping around and multiplying like cockroaches!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . it11.10
- It doesn't matter which -
if you stretch it out you have to pull
in the same direction as it moves,
while if you compress it you have to push
in the direction of motion, so either way
the force and the displacement are in the same direction
and you do positive work on the spring.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . .
comfortable11.11
- Sadly, x0 is not always the same
for both partners in the relationship; this is a leading
cause of tension in such cases. [Doesn't this
metaphor extend gracefully?]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . limit.11.12
- I
suspect that such foolishness is merely an example of
single-valued logic [closer = better] obsessively misapplied,
rather than some more insidious psychopathology.
But I could be wrong!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . zero?11.13
- The choice
of a zero point for Vg is arbitrary, of course,
just like our choice of where h = 0.
This is not a problem if we allow negative
potential energies [which we do!] since it is only the
change in potential energy that appears in any
actual mechanics problem.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . energy.11.14
- [Not
quite, but you can visualize lots of little atoms
wiggling and jiggling seemingly at random - that's heat, sort of.]
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . origin11.15
- Note that everything we discuss
in this case will be with reference to the chosen origin O,
which may be chosen arbitrarily but must then be carefully remembered!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . zero.11.16
- Remember from the chapter on VECTORS
that only the perpendicular parts of two vectors
contribute to the cross product. Any two
parallel vectors have zero cross product.
A vector crossed with itself is the simplest example.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . physics.11.17
- For
instance, the electrostatic force between two
point charges obeys exactly the same "inverse square law"
as gravitation, except with a much stronger constant of proportionality
and the inclusion of both positive and negative charges.
We will have lots more to do with that later on!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- . . . still!11.18
- This
is pretty boring from a Physicist's point of view,
but even Physicists are grateful when bridges do not collapse.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
