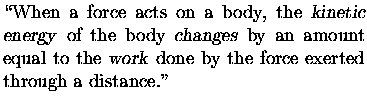

Next: Example: The Hill
Up: The Emergence of Mechanics
Previous: Centre of Mass Velocity
We have seen how much fun it is to multiply the SECOND LAW
by a scalar (dt) and integrate the result.
What if we try multiplying through by a vector?
As we have seen in the chapter on VECTORS, there are
two ways to do this: the scalar or "dot" product
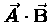 ,
so named for the symbol
,
so named for the symbol  between the two vectors, which yields a scalar result,
and the vector or "cross" product
between the two vectors, which yields a scalar result,
and the vector or "cross" product
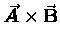 ,
whose name also reflects the appearance of the symbol
,
whose name also reflects the appearance of the symbol 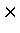 between the two vectors, which yields a vector result.
The former is easier, so let's try it first.
between the two vectors, which yields a vector result.
The former is easier, so let's try it first.
In anticipation of situations where the applied force
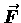 is an explicit function of the position11.5
is an explicit function of the position11.5
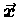 -- i.e.
-- i.e.
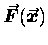 -
let's try using a differential change in
-
let's try using a differential change in
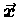 as our multiplier:
as our multiplier:
where we have used the definitions of
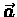 and
and
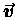 with a little shifting about of the differential dt
and a reordering of the dot product [which we may always do]
to get the right-hand side [RHS] of the equation in the desired form.
A delightful consequence of this form is that it allows us
to convert the RHS into an explicitly scalar form:
with a little shifting about of the differential dt
and a reordering of the dot product [which we may always do]
to get the right-hand side [RHS] of the equation in the desired form.
A delightful consequence of this form is that it allows us
to convert the RHS into an explicitly scalar form:
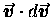 is zero if
is zero if
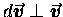 -- i.e. if the change in velocity is perpendicular
to the velocity itself, so that the magnitude of the
velocity does not change, only the direction.
[Recall the case of circular motion!]
If, on the other hand,
-- i.e. if the change in velocity is perpendicular
to the velocity itself, so that the magnitude of the
velocity does not change, only the direction.
[Recall the case of circular motion!]
If, on the other hand,
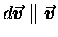 ,
then the whole effect of
,
then the whole effect of
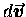 is to change the magnitude of
is to change the magnitude of
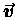 ,
not its direction.
Thus
,
not its direction.
Thus
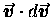 is precisely a measure
of the speed v times the differential
change in speed, dv:
is precisely a measure
of the speed v times the differential
change in speed, dv:
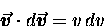 |
(11.6) |
so that our equation can now be written
and therefore
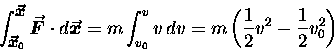 |
(11.7) |
(Recall the earlier discussion of an equivalent antiderivative.)
Just to establish the connection to the mathematical identity
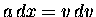 , we multiply that equation through by m
and get
, we multiply that equation through by m
and get
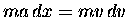 .
Now, in one dimension
(no vectors needed) we know to set ma = F which gives us
.
Now, in one dimension
(no vectors needed) we know to set ma = F which gives us
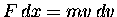 or, integrating both sides,
or, integrating both sides,
which is the same equation in one dimension.
OK, so what?
Well, again this formula kept showing up over and over
when people set out to solve certain types of Mechanics problems,
and again they finally decided to recast the LAW
in this form, giving new names to the left and right sides
of the equation. We call
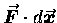 the work dW done by exerting a force
the work dW done by exerting a force
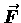 through a distance
through a distance
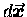 [work is something we do]
and we call
[work is something we do]
and we call
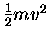 the kinetic energy T.
[kinetic energy is an attribute of a moving mass]
Let's emphasize these definitions:
the kinetic energy T.
[kinetic energy is an attribute of a moving mass]
Let's emphasize these definitions:
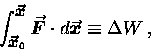 |
(11.8) |
the WORK done by
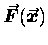 over a path from
over a path from
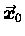 to
to
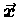 ,
and
,
and
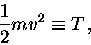 |
(11.9) |
the KINETIC ENERGY of mass m at speed v.
Our equation can then be read as a sentence:
One nice thing about this "paradigm transformation"
is that we have replaced a vector equation
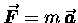 by a scalar equation
by a scalar equation
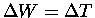 .
There are many situations in which the work done is easily calculated
and the direction of the final velocity is obvious;
one can then obtain the complete "final state"
from the "initial state" in one quick step
without having to go through the details
of what happens in between.
Another class of "before & after" problems solved!
.
There are many situations in which the work done is easily calculated
and the direction of the final velocity is obvious;
one can then obtain the complete "final state"
from the "initial state" in one quick step
without having to go through the details
of what happens in between.
Another class of "before & after" problems solved!


Next: Example: The Hill
Up: The Emergence of Mechanics
Previous: Centre of Mass Velocity
Jess H. Brewer -
Last modified: Sat Nov 14 12:42:29 PST 2015
![]() ,
so named for the symbol
,
so named for the symbol ![]() between the two vectors, which yields a scalar result,
and the vector or "cross" product
between the two vectors, which yields a scalar result,
and the vector or "cross" product
![]() ,
whose name also reflects the appearance of the symbol
,
whose name also reflects the appearance of the symbol ![]() between the two vectors, which yields a vector result.
The former is easier, so let's try it first.
between the two vectors, which yields a vector result.
The former is easier, so let's try it first.
![]() is an explicit function of the position11.5
is an explicit function of the position11.5
![]() -- i.e.
-- i.e.
![]() -
let's try using a differential change in
-
let's try using a differential change in
![]() as our multiplier:
as our multiplier:
![]() , we multiply that equation through by m
and get
, we multiply that equation through by m
and get
![]() .
Now, in one dimension
(no vectors needed) we know to set ma = F which gives us
.
Now, in one dimension
(no vectors needed) we know to set ma = F which gives us
![]() or, integrating both sides,
or, integrating both sides,
![]() the work dW done by exerting a force
the work dW done by exerting a force
![]() through a distance
through a distance
![]() [work is something we do]
and we call
[work is something we do]
and we call
![]() the kinetic energy T.
[kinetic energy is an attribute of a moving mass]
Let's emphasize these definitions:
the kinetic energy T.
[kinetic energy is an attribute of a moving mass]
Let's emphasize these definitions: