
Next: Love as a Spring
Up: Work and Energy
Previous: Example: The Hill
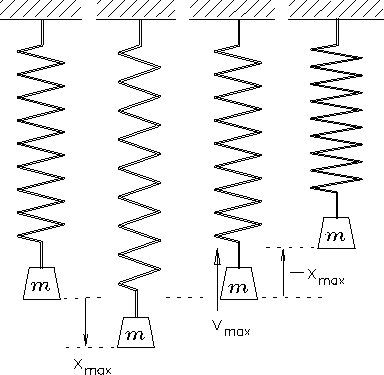
Figure:
Sketch of a mass on a spring.
In the leftmost frame the mass m is at rest and the spring
is in its equilibrium position
( i.e. neither stretched nor compressed).
[If gravity is pulling the mass down, then in the equilibrium position
the spring is stretched just enough to counteract the force of gravity.
The equilibrium position can still be taken
to define the x=0 position.]
In the second frame, the spring has been gradually pulled down
a distance
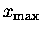 and the mass is once again at rest.
Then the mass is released and accelerates upward under the
influence of the spring until it reaches the equilibrium position
again [third frame]. This time, however, it is moving at its
maximum velocity
and the mass is once again at rest.
Then the mass is released and accelerates upward under the
influence of the spring until it reaches the equilibrium position
again [third frame]. This time, however, it is moving at its
maximum velocity
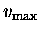 as it crosses the centre position;
as soon as it goes higher, it compresses the spring and
begins to be decelerated by a linear restoring force in the
opposite direction. Eventually, when
as it crosses the centre position;
as soon as it goes higher, it compresses the spring and
begins to be decelerated by a linear restoring force in the
opposite direction. Eventually, when
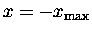 ,
all the kinetic energy has been been stored back up in the compression
of the spring and the mass is once again instantaneously at rest
[fourth frame]. It immediately starts moving downward again at
maximum acceleration and heads back toward its starting point.
In the absence of friction, this cycle will repeat forever.
,
all the kinetic energy has been been stored back up in the compression
of the spring and the mass is once again instantaneously at rest
[fourth frame]. It immediately starts moving downward again at
maximum acceleration and heads back toward its starting point.
In the absence of friction, this cycle will repeat forever.
 |
The spring embodies one of Physics' premiere paradigms,
the linear restoring force. That is, a force which disappears
when the system in question is in its "equilibrium position"
x0 [which we will define as the x = 0 position
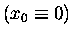 to make the calculations easier]
but increases as x moves away from equilibrium,
in such a way that the magnitude of the force F
is proportional to the displacement from equilibrium
[F is linear in x] and the direction
of F is such as to try to restore x to
the original position. The constant of proportionality
is called the spring constant, always written k.
Thus (using vector notation to account for the directionality)
to make the calculations easier]
but increases as x moves away from equilibrium,
in such a way that the magnitude of the force F
is proportional to the displacement from equilibrium
[F is linear in x] and the direction
of F is such as to try to restore x to
the original position. The constant of proportionality
is called the spring constant, always written k.
Thus (using vector notation to account for the directionality)
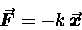 |
(11.11) |
which is the mathematical expression of the concept of a
linear restoring force.
This is known as HOOKE'S LAW.
It is a lot more general than it looks,
as we shall see later.
Keeping in mind that the
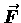 given above is the force exerted by the spring
against anyone or anything trying to stretch or compress it.
If you are that stretcher/compressor, the force you exert is
given above is the force exerted by the spring
against anyone or anything trying to stretch or compress it.
If you are that stretcher/compressor, the force you exert is
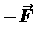 .
If you do work on the spring11.9
by stretching or compressing it11.10
by a differential displacement
.
If you do work on the spring11.9
by stretching or compressing it11.10
by a differential displacement
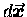 from equilibrium,
the differential amount of work done is given by
from equilibrium,
the differential amount of work done is given by
which we can integrate from x = 0 (the equilibrium position)
to x (the final position) to get the net work W:
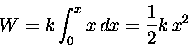 |
(11.12) |
Once you let go, the spring will do the same amount of work back
against the only thing trying to impede it - namely, the inertia
of the mass m attached to it.
This can be used with the WORK AND ENERGY Law
to calculate the speed
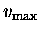 in the third frame of Fig. 11.4: since v0 = 0,
in the third frame of Fig. 11.4: since v0 = 0,
where
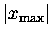 denotes the absolute value
of
denotes the absolute value
of
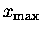 (i.e. its magnitude, always positive).
Note that this is a relationship between the maximum
values of v and x, which occur at different times
during the process.
(i.e. its magnitude, always positive).
Note that this is a relationship between the maximum
values of v and x, which occur at different times
during the process.


Next: Love as a Spring
Up: Work and Energy
Previous: Example: The Hill
Jess H. Brewer -
Last modified: Sat Nov 14 12:43:13 PST 2015


![]() to make the calculations easier]
but increases as x moves away from equilibrium,
in such a way that the magnitude of the force F
is proportional to the displacement from equilibrium
[F is linear in x] and the direction
of F is such as to try to restore x to
the original position. The constant of proportionality
is called the spring constant, always written k.
Thus (using vector notation to account for the directionality)
to make the calculations easier]
but increases as x moves away from equilibrium,
in such a way that the magnitude of the force F
is proportional to the displacement from equilibrium
[F is linear in x] and the direction
of F is such as to try to restore x to
the original position. The constant of proportionality
is called the spring constant, always written k.
Thus (using vector notation to account for the directionality)
![]() given above is the force exerted by the spring
against anyone or anything trying to stretch or compress it.
If you are that stretcher/compressor, the force you exert is
given above is the force exerted by the spring
against anyone or anything trying to stretch or compress it.
If you are that stretcher/compressor, the force you exert is
![]() .
If you do work on the spring11.9
by stretching or compressing it11.10
by a differential displacement
.
If you do work on the spring11.9
by stretching or compressing it11.10
by a differential displacement
![]() from equilibrium,
the differential amount of work done is given by
from equilibrium,
the differential amount of work done is given by