BELIEVE   ME   NOT!    -     A   SKEPTIC's   GUIDE  

The Bohr Radius

We can play more games with Bohr's hydrogen atom if we like, using just Eq. (8) to relate r_n and p_n. Suppose we ask, "What is keeping the electron in its orbit?" The answer is, of course, "The Coulomb force of attraction between the positive nucleus and the negative electron!" This centripetal force has the value (in SI units)

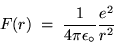$$F(r) \; = \; {1 \over 4 \pi \epsilon_\circ} {e^2 \over r^2}$$ (24.10)

where 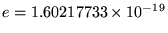$e = 1.60217733 \times 10^{-19}$ C is the magnitude of the charge on either an electron (-e) or a proton (+e) and the ugly mess out front is the legacy of SI units - a constant stuck in to make it come out right. The corresponding electrostatic potential energy is

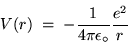$$V(r) \; = \; - {1 \over 4 \pi \epsilon_\circ} {e^2 \over r}$$ (24.11)

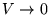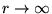(relative to $V \to 0$ at $r \to \infty$). We'll need that momentarily.

A simple application of NEWTON'S SECOND LAW gives

$$m {v^2 \over r} \; = \; {p^2 \over m r} \; = \; {1 \over 4 \pi \epsilon_\circ} {e^2 \over r^2}$$

where m is the mass of the electron. Cancelling one r and rearranging gives

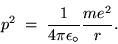$$p^2 \; = \; {1 \over 4 \pi \epsilon_\circ} {m e^2 \over r} .$$ (24.12)

Substituting Eq. (8) into Eq. (12) gives

$$\left( n \hbar \over r_n \right)^2 \; = \; {1 \over 4 \pi \epsilon_\circ} {m e^2 \over r_n}$$

or (after some shuffling)

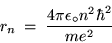$$r_n \; = \; { 4 \pi \epsilon_\circ n^2 \hbar^2 \over m e^2 }$$ (24.13)

for the radius of the $n^{\rm th}$ Bohr orbit of the H atom. The lowest orbit (n = 1) has a special name and symbol: the BOHR RADIUS,

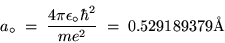$$a_\circ \; = \; { 4 \pi \epsilon_\circ \hbar^2 \over m e^2 } \; = \; 0.529189379 \hbox{\rm\AA}$$ (24.14)

where 1 Å = 10^-10 m.