In defining the concept of temperature,
we have examined the behaviour of systems in thermal contact
(i.e. able to exchange energy back and forth)
when the total energy U is fixed.
In the real world, however, it is not often that we know
the total energy of an arbitrary system;
there is no "energometer" that we can stick into a system
and read off its energy!
What we often do know
about a system it its temperature.
To find this out, all we have to do is
stick a calibrated thermometer into the system
and wait until equilibrium is established
between the thermometer and the system.
Then we read its temperature off the thermometer.
So what can we say about a small system15.23
![]() (like a single molecule)
in thermal equilibrium with a large system
(which we usually call a "heat reservoir"
(like a single molecule)
in thermal equilibrium with a large system
(which we usually call a "heat reservoir" ![]() )
at temperature
)
at temperature
![]() ?
?
Well, the small system can be in any one
of a large number of fully-specified states.
It is convenient to be invent an abstract label
for a given fully-specified state so that we can
talk about its properties and probability.
Let's call such a state
![]() where
where
![]() is a "full label" - i.e.
is a "full label" - i.e.
![]() includes all the information there is
about the state of
includes all the information there is
about the state of ![]() .
It is like a complete
list of which car is parked in which space,
or exactly which coins came up heads or tails
in which order, or whatever. For something simple
like a single particle's spin,
.
It is like a complete
list of which car is parked in which space,
or exactly which coins came up heads or tails
in which order, or whatever. For something simple
like a single particle's spin, ![]() may only
specify whether the spin is up or down.
Now consider some particular fully-specified state
may only
specify whether the spin is up or down.
Now consider some particular fully-specified state
![]() whose energy is
whose energy is
![]() .
As long as
.
As long as ![]() is very big
and
is very big
and ![]() is very small,
is very small,
![]() can - and sometimes will -
absorb from
can - and sometimes will -
absorb from ![]() the energy
the energy
![]() required to be in the state
required to be in the state
![]() ,
no matter how large
,
no matter how large
![]() may be.
However, you might expect that states with
really big
may be.
However, you might expect that states with
really big
![]() would be excited somewhat less often than
states with small
would be excited somewhat less often than
states with small
![]() ,
because the extra energy has to come from
,
because the extra energy has to come from ![]() ,
and every time we take energy out of
,
and every time we take energy out of ![]() we decrease its entropy and make the resultant
configuration that much less probable.
You would be right. Can we be quantitative about this?
we decrease its entropy and make the resultant
configuration that much less probable.
You would be right. Can we be quantitative about this?
Well, the combined system
![]() has a multiplicity function
has a multiplicity function ![]() which is the
product of the multiplicity function
which is the
product of the multiplicity function
![]() for
for ![]() [which equals 1 because we have already postulated that
[which equals 1 because we have already postulated that
![]() is in a specific fully specified
state
is in a specific fully specified
state
![]() ]
and the multiplicity function
]
and the multiplicity function
![]() for
for ![]() :
:
The energy of the reservoir ![]() before we brought
before we brought
![]() into contact with it was U.
We don't need to know the value of U,
only that it was a fixed starting point.
The entropy of
into contact with it was U.
We don't need to know the value of U,
only that it was a fixed starting point.
The entropy of ![]() was then
was then
![]() .
Once contact is made and an energy
.
Once contact is made and an energy
![]() has been "drained off" into
has been "drained off" into ![]() ,
the energy of
,
the energy of ![]() is
is
![]() and its entropy is
and its entropy is
![]() .
.
Because
![]() is so tiny
compared to U, we can treat it as a "differential"
of U (like "dU") and estimate the resultant
change in
is so tiny
compared to U, we can treat it as a "differential"
of U (like "dU") and estimate the resultant
change in
![]() [relative to its old value
[relative to its old value
![]() ]
in terms of the derivative of
]
in terms of the derivative of
![]() with respect to energy:
with respect to energy:
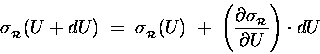
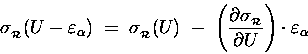
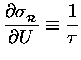 .
Thus
.
Thus