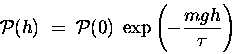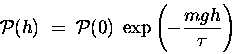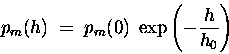

Next: How Big are Atoms?
Up: The Boltzmann Distribution
Previous: The Boltzmann Distribution
The gravitational potential energy of a gas molecule
of mass m at an altitude h above sea level is given
approximately by
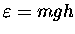 ,
where g = 9.81 m/s2.
Here we neglect the decrease of g with altitude,
which is a good approximation over a few dozen miles.
Next we pretend that the temperature of the
atmosphere does not vary with altitude, which is untrue,
but perhaps relative to 0 K it is not all that silly, since
the difference between the freezing (273.15 K) and
boiling (373.15 K) points of water is less than 1/3 of
their average. For convenience we will assume that the
whole atmosphere has a temperature T = 300 K
(a slightly warm "room temperature").
In this approximation, the probability
,
where g = 9.81 m/s2.
Here we neglect the decrease of g with altitude,
which is a good approximation over a few dozen miles.
Next we pretend that the temperature of the
atmosphere does not vary with altitude, which is untrue,
but perhaps relative to 0 K it is not all that silly, since
the difference between the freezing (273.15 K) and
boiling (373.15 K) points of water is less than 1/3 of
their average. For convenience we will assume that the
whole atmosphere has a temperature T = 300 K
(a slightly warm "room temperature").
In this approximation, the probability
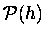 of finding a given molecule
of mass m at height h will drop off
exponentially with h:
of finding a given molecule
of mass m at height h will drop off
exponentially with h:
Thus the density of such molecules per unit volume
and the partial pressure pm of that
species of molecule will drop off exponentially
with altitude h:
where h0 is the altitude at which
the partial pressure has dropped to 1 / e
of its value pm(0) at sea level.
We may call h0 the "mean height of the atmosphere"
for that species of molecule.
A quick comparison and a bit of algebra shows that
For oxygen molecules
(the ones we usually care about most)
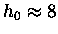 km.
For helium atoms
km.
For helium atoms
 km
and in fact He atoms rise to the "top" of the atmosphere
and disappear into interplanetary space.
This is one reason why we try not to lose any
helium from superconducting magnets etc. -
helium is a non-renewable resource!
km
and in fact He atoms rise to the "top" of the atmosphere
and disappear into interplanetary space.
This is one reason why we try not to lose any
helium from superconducting magnets etc. -
helium is a non-renewable resource!


Next: How Big are Atoms?
Up: The Boltzmann Distribution
Previous: The Boltzmann Distribution
Jess H. Brewer -
Last modified: Mon Nov 16 16:12:28 PST 2015