BELIEVE   ME   NOT!    -     A   SKEPTIC's   GUIDE  

How Big are Atoms?

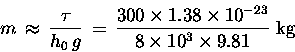
Wait a minute! How did I calculate  h₀?  I had to know  m  for the different molecules, and that requires some knowledge of the sizes of atoms - information that has not yet been set forth in this book! In fact, empirical observations about how fast the pressure of the atmosphere does drop off with altitude could give a pretty good idea of his big atoms are; this isn't how it was done historically, but let's give it a try anyway:

Suppose that, by climbing mountains and measuring the density of oxygen molecules (O₂) as a function of altitude, we have determined empirically that  h₀  for O₂ is about 8,000 m. Then, according to this simple model, it must be true that the mass  m  of an O₂ molecule is about

$$m \, \approx \, { \tau \over h_0 \, g } \, = \, { 300 \time . . . . . . s 10^{-23} \over 8 \times 10^3 \times 9.81 } \hbox{\rm ~kg}$$

$$\hbox{\rm or} \quad m \, \approx \, 5.3 \times 10^{-26} \hbox{\rm ~kg}$$

This is a mighty small mass!

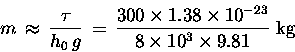
Now to mix in just a pinch of actual history: Long ago, chemists discovered (again empirically) that different pure substances combined with other pure substances in fixed ratios of small integers times a certain characteristic mass (characteristic for each pure substance) called its molecular weight  A.  People had a pretty good idea even then that these pure substances were made up of large numbers of identical units called "atoms,"^15.24 but no one had the faintest idea how big atoms were -- except of course that they must be pretty small, since we never could see any directly. The number  N₀  of molecules in one molecular weight of a pure substance was (correctly) presumed to be the same, to explain why chemical reactions obeyed this rule. This number came to be called a "mole" of the substance. For oxygen (O₂), the molecular weight is roughly 32 grams or 0.032 kg.

If we now combine this conventional definition of a mole of O₂ with our previous estimate of the mass of one O₂ molecule, we can estimate

$$N_0 \; \approx \; { 0.032 \over 5.3 \times 10^{-26} } \; \approx \; 6 \times 10^{23}$$

The exact number, obtained by quite different means, is

$$N_0 \equiv 6.02205 \times 10^{23}$$ (15.17)

molecules per mole. This is known as AVOGADRO'S NUMBER.

Turning the argument around, the mass of a molecule can be obtained from its molecular weight  A  as follows: One mole of any substance is defined as a mass   $A \times 1$ gram, and contains  N₀  molecules (or atoms, in the case of monatomic molecules) of the substance. Thus helium, with  A = 4,  weighs 4 gm (or 0.004 kg) per mole containing  N₀  atoms, so one He atom weighs   (0.004/N₀) kg  or   $6.6 \times 10^{-27}$ kg.