

Next: Interference in Space
Up: Interference
Previous: Interference
Suppose we add together two equal amplitude waves
with slightly different frequencies
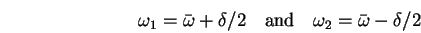 |
(14.44) |
where 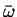 is the average frequency and
is the average frequency and 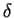 is the difference between the two frequencies.
is the difference between the two frequencies.
Figure:
Beats.
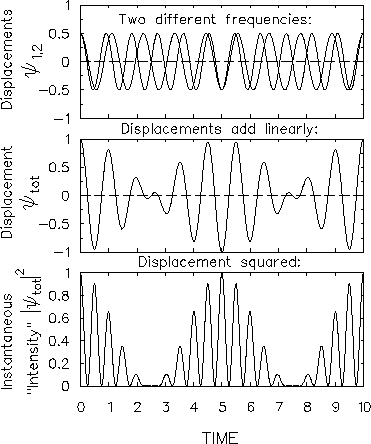 |
If we measure the combined amplitude at a fixed point in space,
a little algebra reveals the phenomenon of BEATS.
This is usually done with 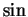 or
or 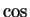 functions
and a lot of trigonometric identities;
let's use the complex notation instead -
I find it more self-evident, at least algebraically:
functions
and a lot of trigonometric identities;
let's use the complex notation instead -
I find it more self-evident, at least algebraically:
That is, the combined signal consists of an oscillation at the
average frequency, modulated by an oscillation at
one-half the difference frequency.
This phenomenon of "BEATS" is familiar to any musician,
automotive mechanic or pilot of a twin engine aircraft.
One seemingly counterintuitive feature of BEATS is that
the "envelope function"
![$\cos [(\delta/2) t]$](img244.png) has only half the
angular frequency of the difference between the two original
frequencies. What we hear when two frequencies interfere
is the variation of the sound INTENSITY with time;
and the intensity is proportional to the square
of the displacement.14.23Squaring the envelope effectively doubles its frequency
(see Fig. 14.12) and so the detected BEAT FREQUENCY
is the full frequency difference
has only half the
angular frequency of the difference between the two original
frequencies. What we hear when two frequencies interfere
is the variation of the sound INTENSITY with time;
and the intensity is proportional to the square
of the displacement.14.23Squaring the envelope effectively doubles its frequency
(see Fig. 14.12) and so the detected BEAT FREQUENCY
is the full frequency difference
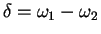 .
.
This is a universal feature of waves and interference:
the detected signal is the average intensity,
which is proportional to the square of
the amplitude of the displacement oscillations;
and it is the displacements themselves that add linearly
to form the interference pattern.
Be sure to keep this straight.
Footnotes
- . . . displacement.14.23
- Actually the INTENSITY
is defined in terms of the average of the
square of the displacement over times long compared with the
average frequency
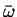 . This makes sense as long as
the beat frequency
. This makes sense as long as
the beat frequency
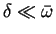 ;
but if
;
but if 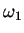 and
and 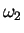 differ by an amount
differ by an amount
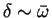 then it is hard to define
what is meant by a "time average".
We will just duck this issue.
then it is hard to define
what is meant by a "time average".
We will just duck this issue.


Next: Interference in Space
Up: Interference
Previous: Interference
Jess H. Brewer -
Last modified: Sun Nov 15 21:36:45 PST 2015
![]() has only half the
angular frequency of the difference between the two original
frequencies. What we hear when two frequencies interfere
is the variation of the sound INTENSITY with time;
and the intensity is proportional to the square
of the displacement.14.23Squaring the envelope effectively doubles its frequency
(see Fig. 14.12) and so the detected BEAT FREQUENCY
is the full frequency difference
has only half the
angular frequency of the difference between the two original
frequencies. What we hear when two frequencies interfere
is the variation of the sound INTENSITY with time;
and the intensity is proportional to the square
of the displacement.14.23Squaring the envelope effectively doubles its frequency
(see Fig. 14.12) and so the detected BEAT FREQUENCY
is the full frequency difference
![]() .
.