

Next: Phasors
Up: Interference
Previous: Interference in Time
Figure:
A replica of Thomas Young's original drawing (1803) showing
the interference pattern created by two similar waves being
emitted "in phase" (going up and down simultaneously)
from two sources separated by a small distance.
The arrows point along lines of constructive interference
(crests on top of crests and troughs underneath troughs)
and the dotted lines indicate "lines of nodes" where
the crests and troughs cancel.
 |
Suppose spherical waves emanate from two point sources
oscillating in phase (one goes "up" at the same time as
the other goes "up") at the same frequency, so that the two
wave-generators are like synchronized swimmers in
water ballet.14.24
Each will produce outgoing spherical waves that will
interfere wherever they meet.
The qualitative situation is pictured in Fig.14.13,
which shows a "snapshot" of two outgoing spherical14.25waves and the "rays" (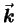 directions) along which
their peaks and valleys (or crests and troughs, whatever) coincide,
giving constructive interference. This diagram accompanied
an experimental observation by Young of "interference fringes""
(a pattern of intensity maxima and minima on a screen some
distance from the two sources) that is generally regarded as
the final proof of the wave nature of light.14.26
directions) along which
their peaks and valleys (or crests and troughs, whatever) coincide,
giving constructive interference. This diagram accompanied
an experimental observation by Young of "interference fringes""
(a pattern of intensity maxima and minima on a screen some
distance from the two sources) that is generally regarded as
the final proof of the wave nature of light.14.26
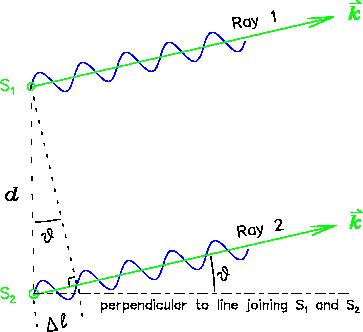
Figure:
Diagram showing the condition for constructive interference
of two "rays" of the same frequency and wavelength 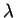 emitted in phase from two sources separated by a distance
emitted in phase from two sources separated by a distance 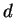 .
At angles for which the difference in path length
.
At angles for which the difference in path length 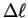 is an integer number (
is an integer number (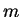 ) of wavelengths,
) of wavelengths, 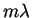 , the two rays
arrive at a distant detector in phase so that their amplitudes
add constructively, maximizing the intensity. The case shown
is for
, the two rays
arrive at a distant detector in phase so that their amplitudes
add constructively, maximizing the intensity. The case shown
is for 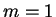 .
.
 |
If we want to precisely locate the angles at which constructive
interference occurs ("interference maxima") then it is most convenient
to think in terms of "rays"
(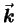 vectors) as pictured in
Fig. 14.14.
vectors) as pictured in
Fig. 14.14.
The mathematical criterion for constructive interference is
simply a statement that the difference in path length,
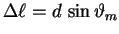 , for the two "rays"
is an integer number
, for the two "rays"
is an integer number  of wavelengths
of wavelengths 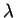 ,
where the
,
where the 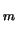 subscript on
subscript on 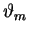 is a reminder
that this will be a different angle for each value of
is a reminder
that this will be a different angle for each value of 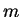 :
:
![\begin{displaymath}
\fbox{ \rule[-0.5\baselineskip]{0pt}{1.5\baselineskip}
\hb . . .
. . . aystyle
d \, \sin \vartheta_m \; = \; m \, \lambda $} }\; .
\end{displaymath}](img261.png) |
(14.46) |
Conversely, if the path length difference is a half-integer
number of wavelengths, the two waves will arrive at the distant
detector exactly out of phase and cancel each other out.
The angles at which this happens are given by
![\begin{displaymath}
\fbox{ \rule[-0.5\baselineskip]{0pt}{1.5\baselineskip}
\hb . . .
. . . r} \; = \;
\left( m + {1\over2} \right) \, \lambda $} }\; .
\end{displaymath}](img263.png) |
(14.47) |
Footnotes
- . . . ballet.14.24
- This notion of being "in phase" or
"out of phase" is one of the most archetypal metaphors in
Physics. It is so compelling that most Physicists incorporate it
into their thinking about virtually everything. A Physicist at a
cocktail party may be heard to say, "Yeah, we were 90
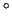 out of phase on everything. Eventually we called it quits."
This is slightly more subtle than, " . . . we were 180
out of phase on everything. Eventually we called it quits."
This is slightly more subtle than, " . . . we were 180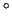 out of phase . . . " meaning diametrically opposed, opposite,
cancelling each other, destructively interfering.
To be "90
out of phase . . . " meaning diametrically opposed, opposite,
cancelling each other, destructively interfering.
To be "90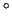 out of phase" means to be moving at top speed
when the other is sitting still (in
out of phase" means to be moving at top speed
when the other is sitting still (in  , this would mean to have
all your energy in kinetic energy when the other has it
all in potential energy) and vice versa.
The
, this would mean to have
all your energy in kinetic energy when the other has it
all in potential energy) and vice versa.
The 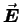 and
and 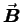 fields in a linearly polarized
fields in a linearly polarized
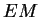 wave are 90
wave are 90 out of phase, as are the "push" and
the "swing" when a resonance is being driven
(like pushing a kid on a swing) at maximum effect,
so in the right circumstances "90
out of phase, as are the "push" and
the "swing" when a resonance is being driven
(like pushing a kid on a swing) at maximum effect,
so in the right circumstances "90 out of phase"
can be productive . . . . Just remember, "in phase" at the
point of interest means constructive interference
(maximum amplitude) and "180
out of phase"
can be productive . . . . Just remember, "in phase" at the
point of interest means constructive interference
(maximum amplitude) and "180 out of phase" at the
point of interest means destructive interference
(minimum amplitude - zero, in fact, if the two waves
have equal amplitude).
out of phase" at the
point of interest means destructive interference
(minimum amplitude - zero, in fact, if the two waves
have equal amplitude).
- . . . spherical14.25
- OK,
they are circular waves, not spherical waves.
You try drawing a picture of spherical waves!
- . . . light.14.26
- Young's
classic experiment is in fact the archetype
for all subsequent demonstrations of wave properties,
as shall be seen in the Chapter(s) on QUANTUM MECHANICS.
Subsections


Next: Phasors
Up: Interference
Previous: Interference in Time
Jess H. Brewer -
Last modified: Sun Nov 15 21:40:36 PST 2015


![]() directions) along which
their peaks and valleys (or crests and troughs, whatever) coincide,
giving constructive interference. This diagram accompanied
an experimental observation by Young of "interference fringes""
(a pattern of intensity maxima and minima on a screen some
distance from the two sources) that is generally regarded as
the final proof of the wave nature of light.14.26
directions) along which
their peaks and valleys (or crests and troughs, whatever) coincide,
giving constructive interference. This diagram accompanied
an experimental observation by Young of "interference fringes""
(a pattern of intensity maxima and minima on a screen some
distance from the two sources) that is generally regarded as
the final proof of the wave nature of light.14.26

![]() , for the two "rays"
is an integer number
, for the two "rays"
is an integer number ![]() of wavelengths
of wavelengths ![]() ,
where the
,
where the ![]() subscript on
subscript on ![]() is a reminder
that this will be a different angle for each value of
is a reminder
that this will be a different angle for each value of ![]() :
: