


Next: Scattering calculations with the
Up: Adiabatic approaches
Previous: Born's Adiabatic method
Adiabatic Representation method
Figure 2.1:
Co-ordinate system for muonic molecular ion  used in
the Adiabatic Representation method.
used in
the Adiabatic Representation method.
 |
The Dubna group, led by Ponomarev, undertook extensive efforts
in the 1970s to solve the muonic three body problem with high accuracy.
Their method, known as the Adiabatic Representation method, is based on the
expansion of the three-body wave function (Eq. 2.12) in the
basis of solutions to the two-centre problem (Eq. 2.13)
describing the muonic motion in the field of two fixed nuclei:
 |
(26) |
where
 indicates summation over the discrete states and integration over continuum
states, and r and R are given in the co-ordinates shown in
Fig. 2.1
indicates summation over the discrete states and integration over continuum
states, and r and R are given in the co-ordinates shown in
Fig. 2.1![[*]](foot_motif.gif) . The basis
. The basis  is given by solving (in the units
is given by solving (in the units
 )
)
![\begin{displaymath}
\left[ -\frac{1}{2m_{a}}\Delta _{r} -\frac {1}{r_{a}} -\frac {1}{r_{b}}
\right] = \epsilon _{j} \phi _{j} (r; R),
\end{displaymath}](img184.gif) |
(27) |
where the reduced mass is defined with respect to one of the nuclei
Ma (
 ):
):
 |
(28) |
such that the energy  is measured from the ground
state of an isolated atom
is measured from the ground
state of an isolated atom  .
The right hand side of
Eq. 2.13 is replaced by
.
The right hand side of
Eq. 2.13 is replaced by
 for the continuum spectrum. The equation for the nuclear wave functions
for the continuum spectrum. The equation for the nuclear wave functions
 is given by an infinite set of coupled
integro-differential
is given by an infinite set of coupled
integro-differential![[*]](foot_motif.gif) equations:
equations:
![\begin{displaymath}
\left[ \frac {d^{2}}{dR^{2}} + \lambda - U_{ii} (R) \right]...
...\sum _{j\neq i}\!\!\!\!\!\!\! \int
\; U_{ij}(R) \chi _{j}(R).
\end{displaymath}](img190.gif) |
(29) |
where Uij are the effective potentials due to the kinetic energy of
the nuclear motion and its coupling to the muon motion, and  are
the eigenvalues, from which the binding energies are derived. Note that
simplified notations given in Ref. [95] are shown here; for the
complete formulae, see a detailed review [96].
Equation 2.15 is similar to the starting point of the Born
approximation derivation (Eq. 2.8),
but contrary to the approximation made in
Eq. 2.10, the non-adiabacity is fully taken into account by
the off-diagonal coupling terms Uij.
are
the eigenvalues, from which the binding energies are derived. Note that
simplified notations given in Ref. [95] are shown here; for the
complete formulae, see a detailed review [96].
Equation 2.15 is similar to the starting point of the Born
approximation derivation (Eq. 2.8),
but contrary to the approximation made in
Eq. 2.10, the non-adiabacity is fully taken into account by
the off-diagonal coupling terms Uij.
Ponomarev and his colleagues overcame the computational challenges (and
limited computer resources at the time) and solved Eq. 2.15 via
systematic expansion in the finite set of the basis functions where
the continuum spectra are discretized via:
 |
(30) |
which gives a truncated system of coupled integro-differential equations
with finite number N. In contrast to the Born Adiabatic method, where
accuracy was not well determined, the convergence of the expansion can be
tested, and the solution was obtained with a controlled
accuracy [96]. With a few hundred basis functions, the solution
converged, giving an accuracy of 10-1 eV [97]. Thus, they
showed for the first time the existence of the loosely bound state for the
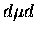 and
and 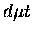 molecules. In fact, for the loosely bound states,
contributions from off-diagonal terms from both discrete and continuum
states are significant [97], and this is why earlier adiabatic
calculations failed to see such states.
molecules. In fact, for the loosely bound states,
contributions from off-diagonal terms from both discrete and continuum
states are significant [97], and this is why earlier adiabatic
calculations failed to see such states.



Next: Scattering calculations with the
Up: Adiabatic approaches
Previous: Born's Adiabatic method


![[*]](foot_motif.gif) . The basis
. The basis 
![[*]](foot_motif.gif) equations:
equations: