


Next: Formulation of the formation
Up: Resonant molecular formation
Previous: Resonant molecular formation
As mentioned earlier, resonant molecular formation refers
to the process:
![\begin{displaymath}
(\mu t)_F + [D_2]_{\nu _{i}, K_{i}} \rightarrow
[(d\mu t)^{S}_{Jv}dee]_{\nu _{f},K_{f}},
\end{displaymath}](img249.gif) |
(38) |
where the kinetic energy of 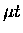 and the energy released
upon formation of
and the energy released
upon formation of 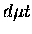 is absorbed in the rotational (K) and
vibrational (
is absorbed in the rotational (K) and
vibrational (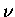 )
excitation of the molecular complex
)
excitation of the molecular complex
![$[(d\mu
t)dee]^{*}$](img250.gif) ,
a hydrogen like molecule with
,
a hydrogen like molecule with 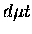 playing the role of one
of the nuclei. The process is resonant in nature because of the discrete
spectra in the final states, corresponding mainly to the ro-vibrational
levels (
playing the role of one
of the nuclei. The process is resonant in nature because of the discrete
spectra in the final states, corresponding mainly to the ro-vibrational
levels (

![[*]](foot_motif.gif) , and the
collision energy has to match the resonant condition. The resonance
condition can be written, when considering purely two body collisions (i.e., neglecting three-body or phonon effects):
, and the
collision energy has to match the resonant condition. The resonance
condition can be written, when considering purely two body collisions (i.e., neglecting three-body or phonon effects):
![\begin{displaymath}
\epsilon _{res} [\mu t + D_2]= \epsilon ^{FS}_{11}[d\mu t] + E_{\nu _f
K_f}[(d\mu t)dee] - E_{\nu _iK_i}[D_2].
\end{displaymath}](img251.gif) |
(39) |
Figure 2.3 gives a schematic energy level
diagram for the resonant 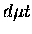 formation process. Plotted on the left
is the potential curve of
formation process. Plotted on the left
is the potential curve of 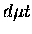 showing the ``shallow'' (in the muonic
scale) bound state, while on the right the molecular complex energy levels
are plotted. Note that due to the reduced mass difference, the energy
levels of D2 and [
showing the ``shallow'' (in the muonic
scale) bound state, while on the right the molecular complex energy levels
are plotted. Note that due to the reduced mass difference, the energy
levels of D2 and [
 ]
are different (by 33.7 meV for the
ground states according to Faifman et al. [138]). In fact
it is this difference in reduced mass which introduces the dependence of
the
]
are different (by 33.7 meV for the
ground states according to Faifman et al. [138]). In fact
it is this difference in reduced mass which introduces the dependence of
the 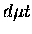 formation rates on the target molecular species, i.e.,
formation rates on the target molecular species, i.e.,
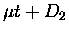 versus
versus  or
or  .
.

Under ordinary target conditions, only
 is populated. On the other
hand, the initial rotational population depends on the target preparation
procedure as well as on temperature. At 3 K, an equilibrated target would
have nearly 100% Ki=0 population (ortho deuterium). Our targets,
however, were prepared by rapidly freezing the statistically populated
deuterium (67% Ki = 0 and 33% Kf = 1) from a hot palladium filter, and
because the rotational relaxation is very slow in the absence of a
catalyst, we expect this population will last for the entire measurement
time. The initial ortho-para population is relevant, because angular
momentum conservation requires:
is populated. On the other
hand, the initial rotational population depends on the target preparation
procedure as well as on temperature. At 3 K, an equilibrated target would
have nearly 100% Ki=0 population (ortho deuterium). Our targets,
however, were prepared by rapidly freezing the statistically populated
deuterium (67% Ki = 0 and 33% Kf = 1) from a hot palladium filter, and
because the rotational relaxation is very slow in the absence of a
catalyst, we expect this population will last for the entire measurement
time. The initial ortho-para population is relevant, because angular
momentum conservation requires:
 |
(40) |
where L is the relative angular momentum in the
reaction (2.24). Since the 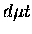 rotational angular
momentum J is 1, we have
rotational angular
momentum J is 1, we have
 for low energy collisions with
L=0 [139]. However, at epithermal energies L>0 becomes
important, allowing various Kf states. This is one of the reasons why we
expect such a high rate at epithermal energies.
for low energy collisions with
L=0 [139]. However, at epithermal energies L>0 becomes
important, allowing various Kf states. This is one of the reasons why we
expect such a high rate at epithermal energies.



Next: Formulation of the formation
Up: Resonant molecular formation
Previous: Resonant molecular formation
![[*]](foot_motif.gif) , and the
collision energy has to match the resonant condition. The resonance
condition can be written, when considering purely two body collisions (i.e., neglecting three-body or phonon effects):
, and the
collision energy has to match the resonant condition. The resonance
condition can be written, when considering purely two body collisions (i.e., neglecting three-body or phonon effects):
![]() is populated. On the other
hand, the initial rotational population depends on the target preparation
procedure as well as on temperature. At 3 K, an equilibrated target would
have nearly 100% Ki=0 population (ortho deuterium). Our targets,
however, were prepared by rapidly freezing the statistically populated
deuterium (67% Ki = 0 and 33% Kf = 1) from a hot palladium filter, and
because the rotational relaxation is very slow in the absence of a
catalyst, we expect this population will last for the entire measurement
time. The initial ortho-para population is relevant, because angular
momentum conservation requires:
is populated. On the other
hand, the initial rotational population depends on the target preparation
procedure as well as on temperature. At 3 K, an equilibrated target would
have nearly 100% Ki=0 population (ortho deuterium). Our targets,
however, were prepared by rapidly freezing the statistically populated
deuterium (67% Ki = 0 and 33% Kf = 1) from a hot palladium filter, and
because the rotational relaxation is very slow in the absence of a
catalyst, we expect this population will last for the entire measurement
time. The initial ortho-para population is relevant, because angular
momentum conservation requires: