



Next: Transverse-Field Measurements
Up: SR Studies of the
Previous: Experimental Setup
Contents
In this chapter, zero-field (ZF) 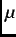 SR measurements on the Pr
SR measurements on the Pr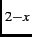 Ce
Ce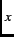 CuO
CuO single crystals are presented. For
all measurements described here, the initial muon-spin polarization
single crystals are presented. For
all measurements described here, the initial muon-spin polarization
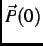 was directed parallel to the CuO
was directed parallel to the CuO layers.
layers.
Figure 4.1 shows the time evolution of the two-counter asymmetry at 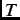 =
= 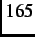 K,
K, 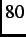 K,
K, 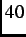 K and
K and 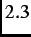 K in
the absence of an external magnetic field. The lack of any discrete frequency oscillations in the ZF-
K in
the absence of an external magnetic field. The lack of any discrete frequency oscillations in the ZF-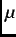 SR signals
indicates that there is no onset of magnetic order at temperatures
SR signals
indicates that there is no onset of magnetic order at temperatures
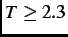 K.
K.
Fig. 4.2:
Time evolution of the asymmetry in longitudinal external magnetic fields of 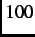 Oe and
Oe and 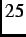 Oe, at
Oe, at 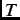 =
= 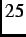 K.
The direction of both the external magnetic field and the initial muon-spin polarization are parallel to the CuO
K.
The direction of both the external magnetic field and the initial muon-spin polarization are parallel to the CuO layers. The scatter in the data is due to low statistics (
layers. The scatter in the data is due to low statistics ( 1 million muon-decay events).
1 million muon-decay events).
|
|
To gain further insight into the nature of the magnetism which relaxes the ZF-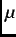 SR signal, a constant magnetic field was
applied along the direction of the initial muon-spin polarization. This arrangement is known as a longitudinal-field
(LF)
SR signal, a constant magnetic field was
applied along the direction of the initial muon-spin polarization. This arrangement is known as a longitudinal-field
(LF) 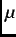 SR experiment. Muons implanted in the sample precesses about the local magnetic field, which is a vector sum of
the applied field and the local internal magnetic fields due to nuclear and electronic magnetic moments. If the internal
magnetic field is static and a large external magnetic field
SR experiment. Muons implanted in the sample precesses about the local magnetic field, which is a vector sum of
the applied field and the local internal magnetic fields due to nuclear and electronic magnetic moments. If the internal
magnetic field is static and a large external magnetic field 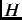 is applied along the direction of the initial
muon-spin polarization
is applied along the direction of the initial
muon-spin polarization
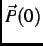 , the component of the resultant magnetic field perpendicular to
, the component of the resultant magnetic field perpendicular to
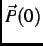 will be
small. Consequently the applied magnetic field decouples the muon spin from the local static magnetic fields [15].
Figure 4.2 shows the time evolution of the asymmetry for applied longitudinal fields of
will be
small. Consequently the applied magnetic field decouples the muon spin from the local static magnetic fields [15].
Figure 4.2 shows the time evolution of the asymmetry for applied longitudinal fields of 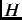 =
= 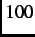 Oe and
Oe and 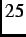 Oe
at
Oe
at 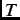 =
= 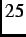 K. A longitudinal field of
K. A longitudinal field of 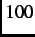 Oe is large enough to completely decouple the muon spin from the local
magnetic field, evident by the non-relaxing asymmetry over the 8
Oe is large enough to completely decouple the muon spin from the local
magnetic field, evident by the non-relaxing asymmetry over the 8 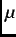 s time range. This indicates that the magnetism in the
sample at
s time range. This indicates that the magnetism in the
sample at 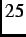 K is fluctuating at a rate of less than
K is fluctuating at a rate of less than  MHz. As the Pr
MHz. As the Pr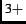 ions have a non-magnetic singlet ground
state and the local magnetic field due to the nuclear magnetic moments is small (i.e.
ions have a non-magnetic singlet ground
state and the local magnetic field due to the nuclear magnetic moments is small (i.e. 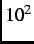 -
-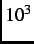 times smaller
than that of the electronic magnetic moments), the dominant source of local magnetism must be from Cu spins.
times smaller
than that of the electronic magnetic moments), the dominant source of local magnetism must be from Cu spins.
The solid curves in Fig. 4.1 are fits to the following relaxation function [26].
![$\displaystyle G(t) = a_1[\frac{1}{3}+\frac{2}{3}(1-\Delta^2 t^2)\exp{((-\Delta^2t^2)/2)}] + a_2\exp{(-\lambda t)}\, ,$](img210.png) |
(5.1) |
where 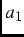 +
+ 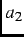 =
= 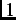 , and
, and 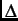 and
and 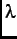 are the Gaussian and exponential relaxation rates, respectively.
Assuming that there is only one muon stopping site, the first term corresponds to the relaxation of the muon-spin
polarization due to muons seeing only nuclear dipole moments. The second term is the relaxation due to muons which see
dilute magnetic moments or magnetic clusters. Figure 4.3 shows the temperature dependence of
are the Gaussian and exponential relaxation rates, respectively.
Assuming that there is only one muon stopping site, the first term corresponds to the relaxation of the muon-spin
polarization due to muons seeing only nuclear dipole moments. The second term is the relaxation due to muons which see
dilute magnetic moments or magnetic clusters. Figure 4.3 shows the temperature dependence of 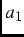 and
and 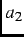 .
The exponential relaxation (i.e.
.
The exponential relaxation (i.e. 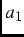 = 0) at high temperature is likely due to ``fast'' fluctuating Cu spins,
although this has not been verified by LF-
= 0) at high temperature is likely due to ``fast'' fluctuating Cu spins,
although this has not been verified by LF- SR measurements. At
SR measurements. At 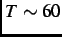 K,
K,
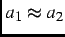 . This indicates that the
dilute magnetic moments are found in 50% of the sample volume. As the temperature is lowered,
. This indicates that the
dilute magnetic moments are found in 50% of the sample volume. As the temperature is lowered, 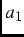 decreases and
decreases and 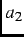 increases, indicating that the dilute magnetic regions grow in size. Figure 4.4 shows the temperature dependence
of the relaxation rates
increases, indicating that the dilute magnetic regions grow in size. Figure 4.4 shows the temperature dependence
of the relaxation rates 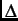 and
and 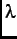 . As the temperature is lowered, the relaxation rates increase monotonically.
This is consistent with a broadening of the magnetic field distribution due to gradual slowing down of the Cu spins.
. As the temperature is lowered, the relaxation rates increase monotonically.
This is consistent with a broadening of the magnetic field distribution due to gradual slowing down of the Cu spins.
Fig. 4.3:
Temperature dependence of the amplitudes 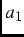 (solid
squares) and
(solid
squares) and 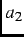 (open circles) from Eq. (4.1). Note that
(open circles) from Eq. (4.1). Note that 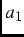 +
+ 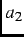 =
= 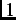 .
.
|
|
Fig. 4.4:
Temperature dependence of the relaxation
rates 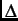 (solid squares) and
(solid squares) and 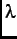 (open circles) from Eq. (4.1).
(open circles) from Eq. (4.1).
|
|




Next: Transverse-Field Measurements
Up: SR Studies of the
Previous: Experimental Setup
Contents
Jess H. Brewer
2003-07-01
![\includegraphics[width=15cm]{zf1.eps}](img204.png) .
.![\includegraphics[width=15cm]{zf1.eps}](img204.png) .
.![]() =
= ![]() K,
K, ![]() K,
K, ![]() K and
K and ![]() K in
the absence of an external magnetic field. The lack of any discrete frequency oscillations in the ZF-
K in
the absence of an external magnetic field. The lack of any discrete frequency oscillations in the ZF-![]() SR signals
indicates that there is no onset of magnetic order at temperatures
SR signals
indicates that there is no onset of magnetic order at temperatures
![]() K.
K.
![\includegraphics[width=14cm]{lf.eps}](img207.png)
![]() SR signal, a constant magnetic field was
applied along the direction of the initial muon-spin polarization. This arrangement is known as a longitudinal-field
(LF)
SR signal, a constant magnetic field was
applied along the direction of the initial muon-spin polarization. This arrangement is known as a longitudinal-field
(LF) ![]() SR experiment. Muons implanted in the sample precesses about the local magnetic field, which is a vector sum of
the applied field and the local internal magnetic fields due to nuclear and electronic magnetic moments. If the internal
magnetic field is static and a large external magnetic field
SR experiment. Muons implanted in the sample precesses about the local magnetic field, which is a vector sum of
the applied field and the local internal magnetic fields due to nuclear and electronic magnetic moments. If the internal
magnetic field is static and a large external magnetic field ![]() is applied along the direction of the initial
muon-spin polarization
is applied along the direction of the initial
muon-spin polarization
![]() , the component of the resultant magnetic field perpendicular to
, the component of the resultant magnetic field perpendicular to
![]() will be
small. Consequently the applied magnetic field decouples the muon spin from the local static magnetic fields [15].
Figure 4.2 shows the time evolution of the asymmetry for applied longitudinal fields of
will be
small. Consequently the applied magnetic field decouples the muon spin from the local static magnetic fields [15].
Figure 4.2 shows the time evolution of the asymmetry for applied longitudinal fields of ![]() =
= ![]() Oe and
Oe and ![]() Oe
at
Oe
at ![]() =
= ![]() K. A longitudinal field of
K. A longitudinal field of ![]() Oe is large enough to completely decouple the muon spin from the local
magnetic field, evident by the non-relaxing asymmetry over the 8
Oe is large enough to completely decouple the muon spin from the local
magnetic field, evident by the non-relaxing asymmetry over the 8 ![]() s time range. This indicates that the magnetism in the
sample at
s time range. This indicates that the magnetism in the
sample at ![]() K is fluctuating at a rate of less than
K is fluctuating at a rate of less than ![]() MHz. As the Pr
MHz. As the Pr![]() ions have a non-magnetic singlet ground
state and the local magnetic field due to the nuclear magnetic moments is small (i.e.
ions have a non-magnetic singlet ground
state and the local magnetic field due to the nuclear magnetic moments is small (i.e. ![]() -
-![]() times smaller
than that of the electronic magnetic moments), the dominant source of local magnetism must be from Cu spins.
times smaller
than that of the electronic magnetic moments), the dominant source of local magnetism must be from Cu spins.
![\includegraphics[width=14cm]{zf2.eps}](img213.png)
![\includegraphics[width=14cm]{zf3.eps}](img214.png)