



Next: SR Spectroscopy
Up: SR Studies of the
Previous: List of Figures
Contents
In 1986, Bednorz and Müller discovered superconductivity in the La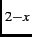 Ba
Ba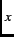 CuO
CuO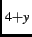 system, below a critical
transition temperature
system, below a critical
transition temperature
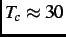 K [1]. This finding was subsequently followed by the discovery of
high-
K [1]. This finding was subsequently followed by the discovery of
high-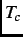 superconductivity in a number of related layered compounds consisting of CuO
superconductivity in a number of related layered compounds consisting of CuO planes. The CuO
planes. The CuO planes
in these materials are separated by ``charge reservoir layers'', which control the oxidation state of the copper ions.
High-
planes
in these materials are separated by ``charge reservoir layers'', which control the oxidation state of the copper ions.
High-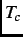 superconductivity is achieved when the undoped parent compound (e.g. La
superconductivity is achieved when the undoped parent compound (e.g. La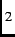 CuO
CuO ), which is an
antiferromagnetic insulator, is doped with holes (Fig. 1.1) [2]. An exception is the
R
), which is an
antiferromagnetic insulator, is doped with holes (Fig. 1.1) [2]. An exception is the
R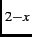 Ce
Ce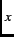 CuO
CuO system, where R = {La, Nd, Pr, Sm or Eu}. In this case, high-
system, where R = {La, Nd, Pr, Sm or Eu}. In this case, high-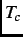 superconductivity occurs
upon partial substitution of Ce
superconductivity occurs
upon partial substitution of Ce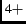 for R
for R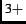 , which dopes electrons into the CuO
, which dopes electrons into the CuO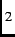 layers. The most studied
electron-doped high-
layers. The most studied
electron-doped high-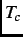 superconductor (HTSC) is Nd
superconductor (HTSC) is Nd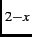 Ce
Ce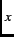 CuO
CuO , which was synthesized by Tokura and
co-workers in 1989 [3]. Compared to hole-doped HTSC's, less is known about the electron-doped cuprates. One
reason is that it is difficult to synthesize high-quality single crystals. In contrast to the hole-doped compounds,
as-grown crystals are made superconducting by subjecting them to an oxygen reduction process [4], which
often degrades the crystal surface. In addition, single crystals of electron-doped cuprates are generally plagued by spatial
inhomogeneity of the cerium and oxygen concentration [5,6].
, which was synthesized by Tokura and
co-workers in 1989 [3]. Compared to hole-doped HTSC's, less is known about the electron-doped cuprates. One
reason is that it is difficult to synthesize high-quality single crystals. In contrast to the hole-doped compounds,
as-grown crystals are made superconducting by subjecting them to an oxygen reduction process [4], which
often degrades the crystal surface. In addition, single crystals of electron-doped cuprates are generally plagued by spatial
inhomogeneity of the cerium and oxygen concentration [5,6].
Fig. 1.1:
Generic Phase diagram of the hole-doped HTSC
La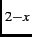 Sr
Sr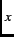 CuO
CuO and the electron-doped HTSC Pr
and the electron-doped HTSC Pr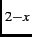 Ce
Ce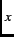 CuO
CuO as a function of charge doping concentration,
showing the anitferromagnetic (AF), spin glass (SG) and superconducting (SC) phases.
as a function of charge doping concentration,
showing the anitferromagnetic (AF), spin glass (SG) and superconducting (SC) phases.
|
|
One of the fundamental properties of superconductors is that they exhibit a diamagnetic response called the ``Meissner
effect.'' When a superconducting material is cooled below 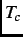 in the presence of a weak applied magnetic field
in the presence of a weak applied magnetic field 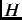 , the
field is expelled from the bulk of the sample. When the applied magnetic field exceeds a critical value
, the
field is expelled from the bulk of the sample. When the applied magnetic field exceeds a critical value 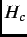 ,
superconductivity is destroyed. For type-II superconductors, like the high-
,
superconductivity is destroyed. For type-II superconductors, like the high-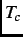 cuprates, the response to an applied
magnetic field can be one of the following:
cuprates, the response to an applied
magnetic field can be one of the following:
- Meissner State: At
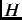 <
< 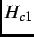 , (where
, (where
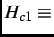 the lower critical magnetic field),
supercurrents circulate near the surface of the sample, screening the magnetic field from the bulk. However, the external
magnetic field partially penetrates the sample at the surface. The magnitude of the penetrating field-component parallel to
the surface decays exponentially [7] as a function of distance from the surface. The characteristic length
scale of the exponential field decay is the ``magnetic penetration depth''
the lower critical magnetic field),
supercurrents circulate near the surface of the sample, screening the magnetic field from the bulk. However, the external
magnetic field partially penetrates the sample at the surface. The magnitude of the penetrating field-component parallel to
the surface decays exponentially [7] as a function of distance from the surface. The characteristic length
scale of the exponential field decay is the ``magnetic penetration depth'' 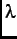 . This quantity is of fundamental
importance, as
. This quantity is of fundamental
importance, as
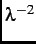 is proportional to the density of superconducting carriers
is proportional to the density of superconducting carriers 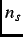 .
.
- Vortex State: At
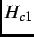 <
< 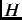 <
< 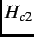 (where
(where
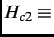 the upper critical magnetic field),
magnetic flux penetrates the bulk of the superconductor in the form of a periodic arrangement of quantized flux lines,
called a ``vortex lattice''. Each vortex in the lattice is comprised of one flux quantum
the upper critical magnetic field),
magnetic flux penetrates the bulk of the superconductor in the form of a periodic arrangement of quantized flux lines,
called a ``vortex lattice''. Each vortex in the lattice is comprised of one flux quantum 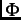 =
= 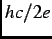 . The vortex core
is a region where the ``superconducting order parameter''
. The vortex core
is a region where the ``superconducting order parameter'' 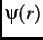 is suppressed and the local magnetic field
is suppressed and the local magnetic field  is
maximum (
is
maximum (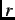 is the radial distance from the centre of the vortex). The length scale which governs spatial variations of
is the radial distance from the centre of the vortex). The length scale which governs spatial variations of
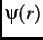 is called the ``superconducting coherence length''
is called the ``superconducting coherence length'' 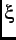 . Supercurrents circulating around the individual vortices
screen the magnetic field within the vortex core from the surrounding material, in the same way that supercurrents near the
sample surface screen the external magnetic field in the Meissner state. Consequently, the magnetic field decays outside the
vortex core region over the length scale
. Supercurrents circulating around the individual vortices
screen the magnetic field within the vortex core from the surrounding material, in the same way that supercurrents near the
sample surface screen the external magnetic field in the Meissner state. Consequently, the magnetic field decays outside the
vortex core region over the length scale 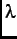 .
.
- Normal State:
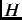 >
> 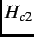 , the external magnetic field fully penetrates the sample and superconductivity
is destroyed.
, the external magnetic field fully penetrates the sample and superconductivity
is destroyed.
One of the outstanding issues concerning the electron-doped HTSCs is the pairing symmetry of the superconducting carriers in
these compounds. While there are phase sensitive [8], angle resolved photoemission spectroscopy
[9] and microwave [10] measurements that suggest the pairing symmetry is
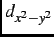 -wave
(like in hole-doped HTSCs), other experiments [11,12] favour
-wave
(like in hole-doped HTSCs), other experiments [11,12] favour 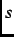 -wave symmetry. Measurements of the
temperature dependence of the magnetic penetration depth are one way of distinguishing between
-wave symmetry. Measurements of the
temperature dependence of the magnetic penetration depth are one way of distinguishing between 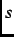 -wave and
-wave and
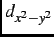 -wave symmetry. Thus far, most measurements of
-wave symmetry. Thus far, most measurements of 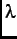 in electron-doped HTSCs have been performed in the
Meissner state. In this thesis, the results of measurements of the in-plane magnetic penetration depth
in electron-doped HTSCs have been performed in the
Meissner state. In this thesis, the results of measurements of the in-plane magnetic penetration depth
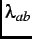 in the
vortex state of the electron-doped HTSC Pr
in the
vortex state of the electron-doped HTSC Pr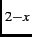 Ce
Ce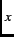 CuO
CuO , by muon spin rotation (
, by muon spin rotation (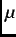 SR) spectroscopy are
presented. As a bulk local probe,
SR) spectroscopy are
presented. As a bulk local probe, 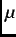 SR has the advantage that it is insensitive to inhomogeneities at the sample
surface. The samples measured are the smallest single crystals studied so far by the
SR has the advantage that it is insensitive to inhomogeneities at the sample
surface. The samples measured are the smallest single crystals studied so far by the 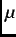 SR techniques.A complication in
studying electron-doped HTSCs, is the electronic magnetic moments of the rare-earth ions. For example, their presence has
prevented an accurate determination of the values of the magnetic penetration depth in the Meissner state
[13,14]. The Pr
SR techniques.A complication in
studying electron-doped HTSCs, is the electronic magnetic moments of the rare-earth ions. For example, their presence has
prevented an accurate determination of the values of the magnetic penetration depth in the Meissner state
[13,14]. The Pr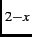 Ce
Ce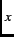 CuO
CuO compound is appealing for study, because the crystal-electric-field
ground state of the Pr ion is non-magnetic.
compound is appealing for study, because the crystal-electric-field
ground state of the Pr ion is non-magnetic.
In the next chapter an introduction to the 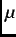 SR method is given. Chapter 3 provides a brief description of the crystal
growth process, sample characteristics and the experimental setup. In Chapters 4 and 5, the experimental results are
presented. A discussion of the results and conclusions are given in Chapter 6.
SR method is given. Chapter 3 provides a brief description of the crystal
growth process, sample characteristics and the experimental setup. In Chapters 4 and 5, the experimental results are
presented. A discussion of the results and conclusions are given in Chapter 6.




Next: SR Spectroscopy
Up: SR Studies of the
Previous: List of Figures
Contents
Jess H. Brewer
2003-07-01
![\includegraphics[width=12cm]{phase-diagram.eps}](img58.png)
![\includegraphics[width=12cm]{phase-diagram.eps}](img58.png)
![]() in the presence of a weak applied magnetic field
in the presence of a weak applied magnetic field ![]() , the
field is expelled from the bulk of the sample. When the applied magnetic field exceeds a critical value
, the
field is expelled from the bulk of the sample. When the applied magnetic field exceeds a critical value ![]() ,
superconductivity is destroyed. For type-II superconductors, like the high-
,
superconductivity is destroyed. For type-II superconductors, like the high-![]() cuprates, the response to an applied
magnetic field can be one of the following:
cuprates, the response to an applied
magnetic field can be one of the following:
![]() -wave
(like in hole-doped HTSCs), other experiments [11,12] favour
-wave
(like in hole-doped HTSCs), other experiments [11,12] favour ![]() -wave symmetry. Measurements of the
temperature dependence of the magnetic penetration depth are one way of distinguishing between
-wave symmetry. Measurements of the
temperature dependence of the magnetic penetration depth are one way of distinguishing between ![]() -wave and
-wave and
![]() -wave symmetry. Thus far, most measurements of
-wave symmetry. Thus far, most measurements of ![]() in electron-doped HTSCs have been performed in the
Meissner state. In this thesis, the results of measurements of the in-plane magnetic penetration depth
in electron-doped HTSCs have been performed in the
Meissner state. In this thesis, the results of measurements of the in-plane magnetic penetration depth
![]() in the
vortex state of the electron-doped HTSC Pr
in the
vortex state of the electron-doped HTSC Pr![]() Ce
Ce![]() CuO
CuO![]() , by muon spin rotation (
, by muon spin rotation (![]() SR) spectroscopy are
presented. As a bulk local probe,
SR) spectroscopy are
presented. As a bulk local probe, ![]() SR has the advantage that it is insensitive to inhomogeneities at the sample
surface. The samples measured are the smallest single crystals studied so far by the
SR has the advantage that it is insensitive to inhomogeneities at the sample
surface. The samples measured are the smallest single crystals studied so far by the ![]() SR techniques.A complication in
studying electron-doped HTSCs, is the electronic magnetic moments of the rare-earth ions. For example, their presence has
prevented an accurate determination of the values of the magnetic penetration depth in the Meissner state
[13,14]. The Pr
SR techniques.A complication in
studying electron-doped HTSCs, is the electronic magnetic moments of the rare-earth ions. For example, their presence has
prevented an accurate determination of the values of the magnetic penetration depth in the Meissner state
[13,14]. The Pr![]() Ce
Ce![]() CuO
CuO![]() compound is appealing for study, because the crystal-electric-field
ground state of the Pr ion is non-magnetic.
compound is appealing for study, because the crystal-electric-field
ground state of the Pr ion is non-magnetic.
![]() SR method is given. Chapter 3 provides a brief description of the crystal
growth process, sample characteristics and the experimental setup. In Chapters 4 and 5, the experimental results are
presented. A discussion of the results and conclusions are given in Chapter 6.
SR method is given. Chapter 3 provides a brief description of the crystal
growth process, sample characteristics and the experimental setup. In Chapters 4 and 5, the experimental results are
presented. A discussion of the results and conclusions are given in Chapter 6.