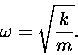BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Limiting Cases
Up: Simple Harmonic Motion
Previous: Imaginary Exponents
Let's take stock. In the previous chapter we found that
satisfies the basic differential equation
defining damped motion (e.g. motion under the influence
of a frictional force proportional to the velocity).
We now have a solution to the equation of motion defining SHM,
where
Can we put these together to "solve" the more general
(and realistic) problem of damped harmonic motion?
The differential equation would then read
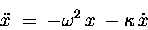 |
(13.20) |
which is beginning to look a little hard.
Still, we can sort it out: the first term on the RHS
says that there is a linear restoring force and an inertial factor.
The second term says that there is a damping force proportional
to the velocity. So the differential equation itself is not
all that fearsome. How can we "solve" it?
As always, by trial and error. Since we have found the
exponential function to be so useful, let's
try one here: Suppose that
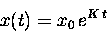 |
(13.21) |
where x0 and K are unspecified constants.
Now plug this into the differential equation and see what we get:
and
The whole thing then reads
which can be true "for all x" only if
which is in the standard form of a general quadratic equation for K,
to which there are two solutions:
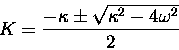 |
(13.22) |
Either of the two solutions given by substituting Eq. (22)
into Eq. (21) will satisfy Eq. (20) describing
damped SHM. In fact, generally any linear combination
of the two solutions will also be a solution.
This can get complicated, but we have found the answer
to a rather broad question.


Next: Limiting Cases
Up: Simple Harmonic Motion
Previous: Imaginary Exponents
Jess H. Brewer -
Last modified: Sun Nov 15 13:37:26 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE