BELIEVE ME NOT! -  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE


Next: Generalization of SHM
Up: Damped Harmonic Motion
Previous: Damped Harmonic Motion
Let's consider a couple of "limiting cases" of such solutions.
First, suppose that the linear restoring force is extremely weak
compared to the "drag" force -
i.e.13.7
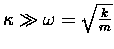 .
Then
.
Then
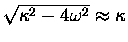 and the solutions are
and the solutions are
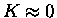 [i.e.
[i.e. 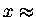 constant, plausible only if x = 0]
and
constant, plausible only if x = 0]
and
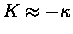 ,
which gives the same sort of
damped behaviour as if there were no restoring force,
which is what we expected.
,
which gives the same sort of
damped behaviour as if there were no restoring force,
which is what we expected.
Now consider the case where the linear restoring force
is very strong and the "drag" force extremely weak -
i.e.
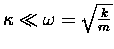 .
Then
.
Then
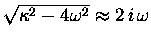 and the solutions are
and the solutions are
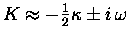 ,
or13.8
,
or13.8
| x(t) |
= |
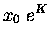 |
(13.23) |
| |
 |
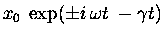 |
(13.24) |
| |
= |
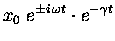 |
(13.25) |
where
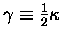 .
We may then think of
.
We may then think of ![$[i \, K]$](img86.gif) as a
complex frequency13.9
whose real part is
as a
complex frequency13.9
whose real part is
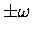 and whose imaginary part is
and whose imaginary part is 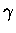 .
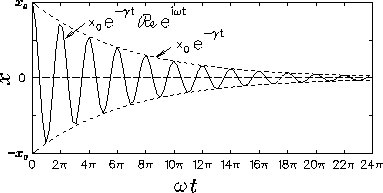
What sort of situation does this describe?
It describes a weakly damped harmonic motion
in which the usual sinusoidal pattern damps away
within an "envelope" whose shape is that of
an exponential decay. A typical case is shown
in Fig. 13.5.
.
What sort of situation does this describe?
It describes a weakly damped harmonic motion
in which the usual sinusoidal pattern damps away
within an "envelope" whose shape is that of
an exponential decay. A typical case is shown
in Fig. 13.5.
Figure:
Weakly damped harmonic motion.
The initial amplitude of x (whatever x is)
is x0, the angular frequency is 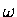 and the damping rate is
and the damping rate is 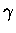 .
The cosine-like oscillation, equivalent to the
real part of
.
The cosine-like oscillation, equivalent to the
real part of
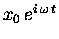 ,
decays within the envelope function
,
decays within the envelope function
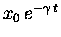 .
.
 |


Next: Generalization of SHM
Up: Damped Harmonic Motion
Previous: Damped Harmonic Motion
Jess H. Brewer -
Last modified: Sun Nov 15 13:49:43 PST 2015
 - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE  - A SKEPTIC's GUIDE
- A SKEPTIC's GUIDE ![]() .
Then
.
Then
![]() and the solutions are
and the solutions are
![]() ,
or13.8
,
or13.8
