

Next: Speed of Propagation
Up: Wave Phenomena
Previous: Wave Phenomena
How do we represent this behaviour mathematically?
Well, 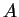 is a function of position
is a function of position 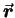 and time
and time 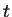 :
: 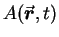 .
At any fixed position
.
At any fixed position 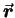 ,
,
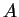 oscillates in time at a frequency
oscillates in time at a frequency 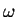 .
We can describe this statement mathematically by saying that
the entire time dependence of
.
We can describe this statement mathematically by saying that
the entire time dependence of 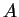 is contained in
[the real part of]
a factor
is contained in
[the real part of]
a factor
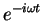 (that is, the amplitude at any fixed position obeys
SHM).14.2
(that is, the amplitude at any fixed position obeys
SHM).14.2
The oscillation with respect to position
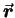 at any instant of time
at any instant of time 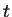 is given by the analogous
factor
is given by the analogous
factor
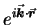 where
where 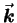 is the wave vector;14.3it points in the direction of propagation of the wave
and has a magnitude (called the "wavenumber")
is the wave vector;14.3it points in the direction of propagation of the wave
and has a magnitude (called the "wavenumber") 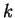 given by
given by
 |
(14.1) |
where 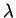 is the wavelength.
Note the analogy between
is the wavelength.
Note the analogy between 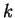 and
and
 |
(14.2) |
where 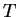 is the period of the oscillation in time
at a given point. You should think of
is the period of the oscillation in time
at a given point. You should think of 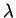 as the "period in space."
as the "period in space."
We may simplify the above description by
choosing our coordinate system so that the 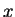 axis
is in the direction of
axis
is in the direction of 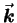 ,
so that14.4
,
so that14.4
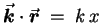 .
Then the amplitude
.
Then the amplitude 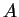 no longer depends on
no longer depends on 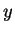 or
or 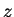 ,
only on
,
only on 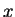 and
and 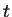 .
.
We are now ready to give a full description of the
function describing this wave:
or, recalling the multiplicative property of the exponential function,
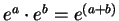 ,
,
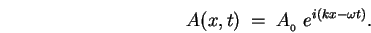 |
(14.3) |
To achieve complete generality we can restore the vector version:
![\begin{displaymath}
\mbox{
\fbox{ \rule[-1.0\baselineskip]{0pt}{2.5\baselineski . . .
. . . eft(
\sVec{k} \cdot \sVec{r} - \omega t
\right)}
}$~
}}
\end{displaymath}](img30.png) |
(14.4) |
This is the preferred form for a general description of a PLANE WAVE,
but for present purposes the scalar version (3) suffices.
Using Eqs. (1) and (2) we can also write the
plane wave function in the form
![\begin{displaymath}
A(x,t) \; = \; A_{_0} \; \exp \left[ 2\pi i \left( {x \over \lambda}
- {t \over T} \right) \right]
\end{displaymath}](img31.png) |
(14.5) |
but you should strive to become completely comfortable with
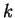 and
and 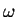 - we will be seeing a lot of them in Physics!
- we will be seeing a lot of them in Physics!
Footnotes
- . . . SHM).14.2
- Note that
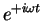 would have worked just as well, since the real part is the same
as for
would have worked just as well, since the real part is the same
as for
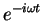 . The choice of sign
does matter, however, when we write down the combined
time and space dependence in Eq. (4), which see.
. The choice of sign
does matter, however, when we write down the combined
time and space dependence in Eq. (4), which see.
- . . . vector;14.3
- The name "wave vector"
is both apt and inadequate - apt because the term vector
explicitly reminds us that its direction defines the direction of
propagation of the wave; inadequate because the essential inverse
relationship between
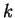 and the wavelength
and the wavelength 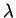 [see Eq. (1)] is not suggested by the name. Too bad.
It is at least a little more descriptive than the name given to
the magnitude
[see Eq. (1)] is not suggested by the name. Too bad.
It is at least a little more descriptive than the name given to
the magnitude 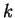 of
of 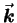 ,
namely the "wavenumber."
,
namely the "wavenumber."
- . . . that14.4
- In general
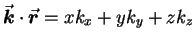 .
If
.
If
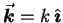 then
then 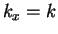 and
and 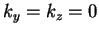 ,
giving
,
giving
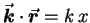 .
.


Next: Speed of Propagation
Up: Wave Phenomena
Previous: Wave Phenomena
Jess H. Brewer -
Last modified: Sun Nov 15 17:57:49 PST 2015
![]() is a function of position
is a function of position ![]() and time
and time ![]() :
: ![]() .
At any fixed position
.
At any fixed position ![]() ,
,
![]() oscillates in time at a frequency
oscillates in time at a frequency ![]() .
We can describe this statement mathematically by saying that
the entire time dependence of
.
We can describe this statement mathematically by saying that
the entire time dependence of ![]() is contained in
[the real part of]
a factor
is contained in
[the real part of]
a factor
![]() (that is, the amplitude at any fixed position obeys
SHM).14.2
(that is, the amplitude at any fixed position obeys
SHM).14.2
![]() at any instant of time
at any instant of time ![]() is given by the analogous
factor
is given by the analogous
factor
![]() where
where ![]() is the wave vector;14.3it points in the direction of propagation of the wave
and has a magnitude (called the "wavenumber")
is the wave vector;14.3it points in the direction of propagation of the wave
and has a magnitude (called the "wavenumber") ![]() given by
given by
![]() axis
is in the direction of
axis
is in the direction of ![]() ,
so that14.4
,
so that14.4
![]() .
Then the amplitude
.
Then the amplitude ![]() no longer depends on
no longer depends on ![]() or
or ![]() ,
only on
,
only on ![]() and
and ![]() .
.