

Next: The Wave Equation
Up: Wave Phenomena
Previous: Traveling Waves
Neither of the images in Fig. 14.1 captures the most important
qualitative feature of the wave: namely, that it propagates
-- i.e. moves steadily along in the direction of
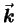 .
If we were to let the snapshot in Fig. 14.1b
become a movie, so that the time dependence could be seen
vividly, what we would see would be the same wave pattern
sliding along the graph to the right at a steady rate.
What rate? Well, the answer is most easily given in
simple qualitative terms:
.
If we were to let the snapshot in Fig. 14.1b
become a movie, so that the time dependence could be seen
vividly, what we would see would be the same wave pattern
sliding along the graph to the right at a steady rate.
What rate? Well, the answer is most easily given in
simple qualitative terms:
The wave has a distance 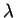 (one wavelength)
between "crests." Every period
(one wavelength)
between "crests." Every period 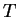 , one full
wavelength passes a fixed position. Therefore a given crest
travels a distance
, one full
wavelength passes a fixed position. Therefore a given crest
travels a distance 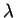 in a time
in a time 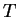 so the velocity
of propagation of the wave is just
so the velocity
of propagation of the wave is just
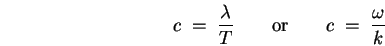 |
(14.6) |
where I have used 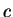 as the symbol for the propagation velocity
even though this is a completely general relationship
between the frequency
as the symbol for the propagation velocity
even though this is a completely general relationship
between the frequency 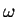 , the wave vector magnitude
, the wave vector magnitude 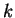 and the propagation velocity
and the propagation velocity 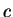 of any sort of wave,
not just electromagnetic waves (for which
of any sort of wave,
not just electromagnetic waves (for which 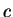 has
its most familiar meaning, namely the speed of light).
has
its most familiar meaning, namely the speed of light).
This result can be obtained more easily by noting that
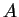 is a function only of the phase
is a function only of the phase
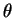 of the oscillation,
of the oscillation,
 |
(14.7) |
and that the criterion for "seeing the same waveform"
is 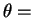 constant or
constant or 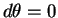 .
If we take the differential of Eq. (7)
and set it equal to zero, we get
.
If we take the differential of Eq. (7)
and set it equal to zero, we get
But 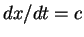 , the propagation velocity of the waveform.
Thus we reproduce Eq. (6).
This treatment also shows why we chose
, the propagation velocity of the waveform.
Thus we reproduce Eq. (6).
This treatment also shows why we chose
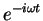 for the
time dependence so that Eq. (7)
would describe the phase: if we used
for the
time dependence so that Eq. (7)
would describe the phase: if we used
 then the
phase would be
then the
phase would be
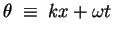 which gives
which gives 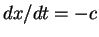 , - i.e. a waveform
propagating in the negative
, - i.e. a waveform
propagating in the negative 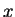 direction
(to the left as drawn).
direction
(to the left as drawn).
If we use the relationship (6) to write
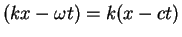 , so that Eq. (4)
becomes
, so that Eq. (4)
becomes
we can extend the above argument to waveforms that are not
of the ideal sinusoidal shape shown in Fig. 14.1;
in fact it is more vivid if one imagines some special
shape like (for instance) a pulse
propagating down a string at velocity 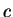 .
As long as
.
As long as 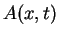 is a function only of
is a function only of 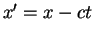 ,
no matter what its shape, it will be static in time
when viewed by an observer traveling along with the wave14.5at velocity
,
no matter what its shape, it will be static in time
when viewed by an observer traveling along with the wave14.5at velocity 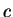 . This doesn't require any elaborate derivation;
. This doesn't require any elaborate derivation;
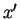 is just the position measured in such an observer's reference frame!
is just the position measured in such an observer's reference frame!
Footnotes
- . . . wave14.5
- Don't
try this with an electromagnetic wave! The argument shown here is
explicitly nonrelativistic, although a more mathematical
proof reaches the same conclusion without such restrictions.


Next: The Wave Equation
Up: Wave Phenomena
Previous: Traveling Waves
Jess H. Brewer -
Last modified: Sun Nov 15 17:58:14 PST 2015
![]() .
If we were to let the snapshot in Fig. 14.1b
become a movie, so that the time dependence could be seen
vividly, what we would see would be the same wave pattern
sliding along the graph to the right at a steady rate.
What rate? Well, the answer is most easily given in
simple qualitative terms:
.
If we were to let the snapshot in Fig. 14.1b
become a movie, so that the time dependence could be seen
vividly, what we would see would be the same wave pattern
sliding along the graph to the right at a steady rate.
What rate? Well, the answer is most easily given in
simple qualitative terms:
![]() (one wavelength)
between "crests." Every period
(one wavelength)
between "crests." Every period ![]() , one full
wavelength passes a fixed position. Therefore a given crest
travels a distance
, one full
wavelength passes a fixed position. Therefore a given crest
travels a distance ![]() in a time
in a time ![]() so the velocity
of propagation of the wave is just
so the velocity
of propagation of the wave is just
![]() is a function only of the phase
is a function only of the phase
![]() of the oscillation,
of the oscillation,
![]() , so that Eq. (4)
becomes
, so that Eq. (4)
becomes