

Next: Energy Density
Up: Linear Superposition
Previous: Standing Waves
None of the foregoing discussion allows us to uniquely specify
any wavelike solution to the WAVE EQUATION, because nowhere have we
given any BOUNDARY CONDITIONS forcing the wave to have any
particular behaviour at any particular point. This is not a problem
for the general phenomenology discussed so far, but if you want to
actually describe one particular wave you have to know this stuff.
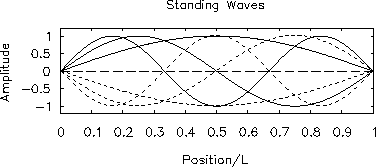
Figure:
The first three allowed standing waves in a
"closed box" (e.g. on a string with fixed ends).
 |
Boundary conditions are probably easiest to illustrate with the system
of a taut string of length 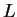 with fixed ends,
as shown in Fig. 14.4.14.6Fixing the ends forces the wave function
with fixed ends,
as shown in Fig. 14.4.14.6Fixing the ends forces the wave function 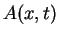 to have nodes
(positions where the amplitude is always zero) at those positions.
This immediately rules out traveling waves and restricts the simple
sinusoidal "modes" to standing waves for which
to have nodes
(positions where the amplitude is always zero) at those positions.
This immediately rules out traveling waves and restricts the simple
sinusoidal "modes" to standing waves for which 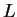 is
an integer number of half-wavelengths:14.7
is
an integer number of half-wavelengths:14.7
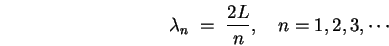 |
(14.19) |
Assuming
that
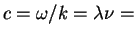 const, the frequency
const, the frequency
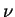 [in cycles per second or Hertz (Hz)]
of the
[in cycles per second or Hertz (Hz)]
of the 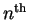 mode is given by
mode is given by
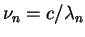 or
or
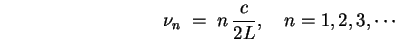 |
(14.20) |
For a string of linear mass density 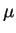 under tension
under tension 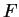 we can use Eq. (16 to write what one might
frivolously describe as THE GUITAR TUNER'S EQUATION:
we can use Eq. (16 to write what one might
frivolously describe as THE GUITAR TUNER'S EQUATION:
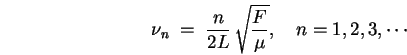 |
(14.21) |
Note that a given string of a given length 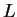 under a given tension
under a given tension 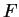 has in principle an infinite number of modes (resonant frequencies);
the guitarist can choose which modes to excite by plucking the string
at the position of an antinode (position of maximum
amplitude) for the desired mode(s). For the first few modes these
antinodes are at quite different places,
as evident from Fig. 14.4.
As another "exercise for the student" try deducing the relationship
between modes with a common antinode - these will all be excited
as "harmonics" when the string is plucked at that position.
has in principle an infinite number of modes (resonant frequencies);
the guitarist can choose which modes to excite by plucking the string
at the position of an antinode (position of maximum
amplitude) for the desired mode(s). For the first few modes these
antinodes are at quite different places,
as evident from Fig. 14.4.
As another "exercise for the student" try deducing the relationship
between modes with a common antinode - these will all be excited
as "harmonics" when the string is plucked at that position.
Exactly the same formulae apply to sound waves
in organ pipes if they are closed at both ends.
An organ pipe open at one end must however have an
antinode at that end; this leads to a slightly different
scheme for enumerating modes, but one that you can easily deduce by
a similar sequence of logic.
This sort of restriction of the allowed modes of a system
to a discrete set of values is known as QUANTIZATION.
However, most people are not accustomed to using that term
to describe macroscopic classical systems like taut strings;
we have a tendency to think of quantization as something that
only happens in QUANTUM MECHANICS.
In reality, quantization is an ubiquitous phenomenon
wherever wave motion runs up against
fixed boundary conditions.
Footnotes
- . . . fig:StandWaves.14.6
- The Figure
could also describe standing sound waves in an organ pipe
closed at both ends, or the electric field strength in a resonant cavity,
or the probability amplitude of an electron confined to a one-dimensional
"box" of length
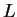 .
.
- . . . half-wavelengths:14.7
- Note that
the
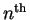 mode has
mode has 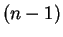 nodes
in addition to the two at the ends.
nodes
in addition to the two at the ends.


Next: Energy Density
Up: Linear Superposition
Previous: Standing Waves
Jess H. Brewer -
Last modified: Sun Nov 15 21:23:43 PST 2015


![]() with fixed ends,
as shown in Fig. 14.4.14.6Fixing the ends forces the wave function
with fixed ends,
as shown in Fig. 14.4.14.6Fixing the ends forces the wave function ![]() to have nodes
(positions where the amplitude is always zero) at those positions.
This immediately rules out traveling waves and restricts the simple
sinusoidal "modes" to standing waves for which
to have nodes
(positions where the amplitude is always zero) at those positions.
This immediately rules out traveling waves and restricts the simple
sinusoidal "modes" to standing waves for which ![]() is
an integer number of half-wavelengths:14.7
is
an integer number of half-wavelengths:14.7