Muon decay electron time spectrum fit

Fits of muon decay electron time spectra to the exponential functions were performed taking into account the finite size of the time bins.

For the muon stopping in M different elements, it obviously holds in the continuous approximation that

where are the numbers of muons in the element k at time t, in which the muon disappearance rate is , and . By solving Eq. C.1 for , we have a number of 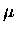$\mu$decay per unit time

where N⁰_k is the number of muons at t=0 in the element k with . Note that Eq. C.2 can be decomposed into a set of M uncoupled independent equations.

On the other hand, the decay electron detection rate, which we measure in our experiments, is

 

= (148)

where is the detector efficiency for decay electrons from the element k, and is the branching ratio of the muon-to-electron decay to total muon disappearance

where is the muon decay rate in free space, and, for the element k, Q_k is the Huff factor, the nuclear capture rate, and is an effective rate representing other loss mechanisms such as muon transfer to heavier elements and muonic atom emission. The Huff factor () takes into account the effect of muon binding to the nucleus, resulting in reduced phase space available as well as the time dilation of the muon's proper time with respect to the lab frame, both of which in turn lead to the reduction in muon decay rate, according to Huff [226]. Thus we have

= (150)

dN^e(t)dt = ddt _k^M N^e_k (t)
& = & _k^M _k Q_k_0Q_k_0 + ^C_k +^X_k_k N^0_k (-_k t)
&=& _k^M _kQ