



Next: Time Differential SR (TD-SR)
Up: SR Spectroscopy
Previous: SR Spectroscopy
Contents
Muons (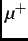 ,
, 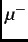 ) can be produced from the parity-violating decay of pions (
) can be produced from the parity-violating decay of pions (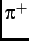 ,
, 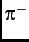 ), which are produced
from the collision of intermediate energy range (
), which are produced
from the collision of intermediate energy range (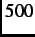 -
-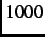 MeV) protons [15] with a low atomic number target
consisting of carbon or beryllium nuclei. Positive pions stopping near the downstream surface of the production target
spontaneously decay after a mean life time of
MeV) protons [15] with a low atomic number target
consisting of carbon or beryllium nuclei. Positive pions stopping near the downstream surface of the production target
spontaneously decay after a mean life time of 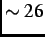 ns via
ns via
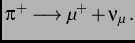 |
(3.1) |
Muons created in this way are called ``surface muons''. Since the neutrino is a left-handed particle (i.e. with its
spin is directed antiparallel to its momentum direction) with spin 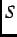 =
=
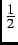 and the pion at rest has a spin
and the pion at rest has a spin 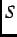 =
0, conservation of linear and angular momentum requires that the decay muon has its spin pointing in a direction opposite
to its linear momentum in the pion rest frame. By collecting the muons traveling in the same direction, a beam with
relatively low kinetic energy (
=
0, conservation of linear and angular momentum requires that the decay muon has its spin pointing in a direction opposite
to its linear momentum in the pion rest frame. By collecting the muons traveling in the same direction, a beam with
relatively low kinetic energy (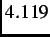 MeV) and a nearly 100% spin polarization is obtained. Thus, unlike conventional
nuclear magnetic resonance (NMR),
MeV) and a nearly 100% spin polarization is obtained. Thus, unlike conventional
nuclear magnetic resonance (NMR), 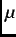 SR benefits from a large initial spin polarization
SR benefits from a large initial spin polarization
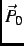 , independent of the
sample or sample environment. Furthermore, as a
, independent of the
sample or sample environment. Furthermore, as a 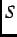 =
=
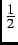 probe, the muon has no electric quadrupole moment and
hence is not directly sensitive to electric field gradients.
probe, the muon has no electric quadrupole moment and
hence is not directly sensitive to electric field gradients.
The muon has a mean lifetime of
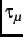 =
= 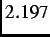
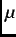 s [16], after which it decays as follows
s [16], after which it decays as follows
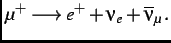 |
(3.2) |
The probability of a decay positron with energy 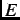 emerging with a momentum at an angle
emerging with a momentum at an angle 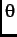 with respect to the
initial muon spin direction is [17]
with respect to the
initial muon spin direction is [17]
![$\displaystyle \begin{eqnarray}dW(\epsilon,\theta)&\propto&(3-2\epsilon)\epsilon . . .
. . . \epsilon)[1+A(\epsilon)\cos\theta]\,d\epsilon\,d(\cos\theta)\, , \end{eqnarray}$](img89.png) |
(3.3a) |
where 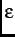 =
= 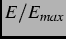 is the reduced energy,
is the reduced energy, 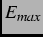 =
=
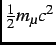 =
= 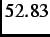 MeV is the maximum
possible relativistic positron energy and
MeV is the maximum
possible relativistic positron energy and
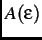 is the asymmetry factor. As shown in Fig. 2.1,
the distribution of decay positrons is asymmetric. The asymmetry is a maximum (i.e.
is the asymmetry factor. As shown in Fig. 2.1,
the distribution of decay positrons is asymmetric. The asymmetry is a maximum (i.e. 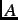 =
= 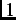 ) when
) when 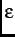 =
= 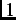 ,
in which case no positrons are emitted antiparallel to the muon spin direction. The high energy positrons easily pass
through components of the experimental apparatus (e.g. cryostat walls). They are detected by counters consisting of
plastic scintillators, light guides and photomultipliers. The detection of the asymmetric distribution of decay positrons
provides a means of determining the time evolution of the spin polarization
,
in which case no positrons are emitted antiparallel to the muon spin direction. The high energy positrons easily pass
through components of the experimental apparatus (e.g. cryostat walls). They are detected by counters consisting of
plastic scintillators, light guides and photomultipliers. The detection of the asymmetric distribution of decay positrons
provides a means of determining the time evolution of the spin polarization
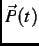 associated with an implanted
ensemble of muons.
associated with an implanted
ensemble of muons.
Fig. 2.1:
Angular
distribution of positrons from the 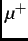 decay with respect to the initial muon spin direction. For
decay with respect to the initial muon spin direction. For
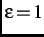 , the asymmetry of the distribution is a maximum. For
, the asymmetry of the distribution is a maximum. For
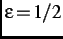 (i.e.
(i.e. 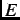 =
= 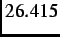 MeV) the
distribution is isotropic.
MeV) the
distribution is isotropic.
|
|




Next: Time Differential SR (TD-SR)
Up: SR Spectroscopy
Previous: SR Spectroscopy
Contents
Jess H. Brewer
2003-07-01
![]() =
= ![]()
![]() s [16], after which it decays as follows
s [16], after which it decays as follows
![\includegraphics[width=10cm]{pos-ang-dist.eps}](img101.png)